决策树的整体理解

什么是决策树

 决策树算法属于监督学习，即原数据必须包含预测变量和目标变量。决策树分为分类决策树（目标变量为分类型数值）和回归决策树（目标变量为连续型变量）。分类决策树叶节点所含样本中，其输出变量的众数就是分类结果；回归树的叶节点所含样本中，其输出变量的平均值就是预测结果。
 与其它分类预测算法不同的是，决策树基于逻辑比较（即布尔比较）。可以简单描述为：If（条件1）Then（结果1）；If（条件2）Then（结果2）。这样，每一个叶节点都对应于一条布尔比较的推理规则，对新数据的预测就正是依靠这些复杂的推理规则。在实际应用中，一个数据产生的推理规则是极为庞大和复杂的，因此对推理规则的精简是需要关注的。

一个例子

数据集如下图所示，它表示的是天气情况与去不去打高尔夫之间的关系。

Day	Outlook	Temperature	Humidity	Windy	Play Golf?
1	Sunny	85	85	False	No
2	Sunny	80	90	True	No
3	Overcast	83	78	False	Yes
4	Rainy	70	96	False	Yes
5	Rainy	68	80	False	Yes
6	Rainy	65	70	True	No
7	Overcast	64	65	True	Yes
8	Sunny	72	95	False	No
9	Sunny	69	70	False	Yes
10	Rainy	75	80	False	Yes
11	Sunny	75	70	True	Yes
12	Overcast	72	90	True	Yes
13	Overcast	81	75	False	Yes
14	Rainy	71	80	True	No

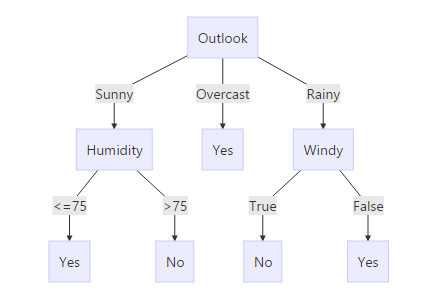
所得到的决策树如下图所示：

决策树的定义

 决策树（decisiontree）是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

决策树的特点

• 决策树是一种树形结构，其中每个内部节点表示在一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。
• 决策树学习是以实例为基础的归纳学习，是一种有监督学习。
• 决策树学习采用的是自顶向下的递归方法，其基本思想是以信息熵为度量构造一颗熵值下降最快的树，到叶子结点处熵为零，此时每个叶节点中的实例都属于同一类。（和梯度下降一样，仍然属于一种Greed算法，也就是说有可能陷入局部最优解。）

决策树的优点

• 易于理解和解释 人们很容易理解决策树的意义。
• 只需很少的数据准备 其他技术往往需要数据归一化。
• 即可以处理数值型数据也可以处理类别型 数据。其他技术往往只能处理一种数据类型。例如关联规则只能处理类别型的而神经网络只能处理数值型的数据。
• 使用白箱 模型. 输出结果容易通过模型的结构来解释。而神经网络是黑箱模型，很难解释输出的结果。
• 可以通过测试集来验证模型的性能 。可以考虑模型的稳定性。
• 强健控制. 对噪声处理有好的强健性。
• 可以很好的处理大规模数据 。

决策树的缺点

• 训练一棵最优的决策树是一个完全NP问题。因此, 实际应用时决策树的训练采用启发式搜索算法例如 贪心算法 来达到局部最优。这样的算法没办法得到最优的决策树。
• 决策树创建的过度复杂会导致无法很好的预测训练集之外的数据。这称作过拟合.[11] 剪枝机制可以避免这种问题。
• 有些问题决策树没办法很好的解决,例如 异或问题。解决这种问题的时候，决策树会变得过大。 要解决这种问题，只能改变问题的领域[12] 或者使用其他更为耗时的学习算法 (例如统计关系学习 或者 归纳逻辑编程).

参考文献

决策树：C5.0（一）

决策树（二）：从零构建决策树及ID3

算法杂货铺——分类算法之决策树(Decision tree)

决策树学习