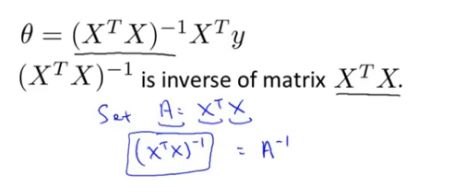【重温经典】吴恩达机器学习课程学习笔记五:特征处理与多项式拟合
【导读】前一段时间,专知内容组推出了春节充电系列:李宏毅2017机器学习课程学习笔记,反响热烈,由此可见,大家对人工智能、机器学习的系列课程非常感兴趣,近期,专知内容组推出吴恩达老师的机器学习课程笔记系列,重温机器学习经典课程,希望大家会喜欢。
【重温经典】吴恩达机器学习课程学习笔记二:无监督学习(unsupervised learning)
【重温经典】吴恩达机器学习课程学习笔记三:监督学习模型以及代价函数的介绍
吴恩达机器学习课程系列视频链接:
http://study.163.com/course/courseMain.htm?courseId=1004570029
吴恩达课程学习笔记六:特征处理与多项式拟合
1、特征的处理与多项式的拟合
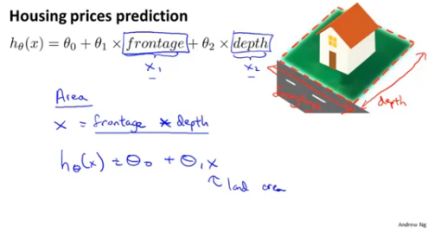
同样是房价预测的例子,如下图所示,对于房价的预测由两个特征决定,即临街宽度(frontage)与纵向深度(depth),根据经验可知,这两个特征可以用一个特征面积来表示(即临街宽度与纵向深度的乘积)。所以预测函数写成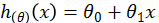
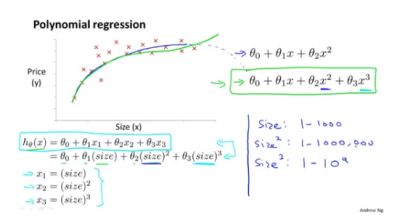
另外,对于像如下所示的数据集,直接线性拟合是不合适的,利用二次函数拟合也是不合适的(因为经验告诉我们,房价不会随着房子面积的增大而下降),故而我们想到用三次函数去拟合。对于三次函数我们可以通过如下方式将其转化为线性拟合:
将size,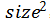
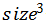
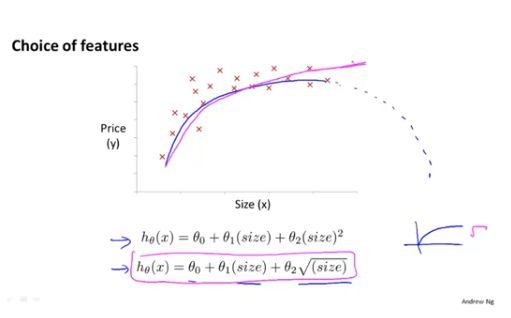
除了用三次函数拟合外,考虑到平方根函数的特点(即随着自变量的增加,最终上升会越来越缓慢),可以将上述数据利用线性函数和平方根函数来拟合。
2、正规方法(区别与迭代算法的直接求解方法)
不同于迭代算法,正规方程法提供了一种求解最优参数的解析解法,可以一次性直接求出最优参数。
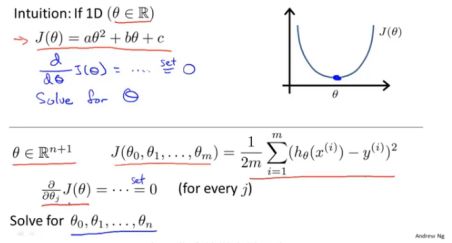
首先我们从一个很简单的代价函数入手,如下:
1、 假设代价函数是标量θ的二次函数,则只需要对其求导,令求导后的值为零,反解出θ即为最优参数值。(针对的是线性回归)
2、 若θ为向量,则可以对每一个进行求导,令其为0,求解出向量θ。但这往往可能是复杂的。
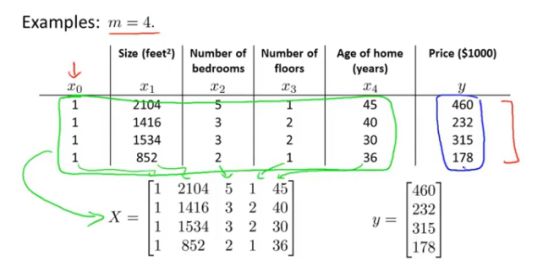
通过把数据用矩阵以及向量来表示,可以更方便进行求解。
对于数据的表示如下所示,添加一列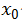
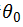
对于线性回归的最优参数,可以利用下图所示的式子进行求解(数学上已经得到证明):
注意利用正规方程法进行求解最优参数时,尽管特征的取值范围可能会有很大差别,但是不需要对特征进行特征缩放。
下面给出梯度下降算法以及正规方程法的优缺点,以便在实际中去选择合适的算法。(假设这里有m条样本,n种特征)
梯度下降的缺点&正规方程法的优点:
对于梯度下降算法来说,它需要选择学习率α,并且需要通过对比不同的α在不同迭代次数后,J(θ)的收敛情况来决定哪一个α的值更合适。但对于正规方程法这是不需要的。
梯度下降的优点&正规方程法的缺点:
即使特征种类n数值很大,梯度下降法也可以很好地运行,最终求解出最优参数θ,但对于正规方程法,因为计算过程中涉及到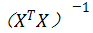
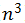
对于n的值对算法选择的影响,课程中给出它的经验是10000以后会考虑使用梯度下降法或者其它的算法。
需要强调一下:对于线性回归问题,我们可以使用正规方程法,但对于后面总结中会介绍的分类问题等,使用正规化方程法可能并不可行,这时梯度 下降法会体现出它的优势。
3、正规方程法在矩阵不可逆的情况下的解决方法
有线性代数基础的读者可能会发现并不是所有矩阵都可以求逆,所以这里将总结出现不可逆的主要情况以及解决方法。
如下所示:
1、可能是众多种类的特征中出现了线性相关的特征(如下,对于面积,用米作为单位以及英尺作为单位的x1与x2同时出现在特征中,这时就可能出现矩阵不可逆的情况)。
2、 特征的种类数过多即样本数小于特征数,则可能会出现不可逆的情况。
解决:
1、 去掉可能线性相关的特征。
2、 在不会影响结果的前提下,去掉一些特征。
3、使用正则化来适应大量的特征。
接下来的总结中将介绍logistic回归的相关知识。
参考链接:
http://study.163.com/course/courseMain.htm?courseId=1004570029
请关注专知公众号(扫一扫最下面专知二维码,或者点击上方蓝色专知),
后台回复“NGML2018” 就可以获取 吴恩达机器学习课程下载链接~
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域26个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
点击“阅读原文”,使用专知