ICML2018论文公布!一文了解机器学习最新热议论文和研究热点
【导读】ICML 2018昨天公布了会议接受论文,各家组织机构和研究大牛们在Twitter上纷纷报喜,放出接受论文,恭喜!有Google Brain、DeepMind、Facebook、微软和各大高校等。专知整理了Twitter上的关注度比较热的一些论文,供大家了解,最新关于机器学习的一些热门研究方向!
Differentiable Dynamic Programming for Structured Prediction and Attention
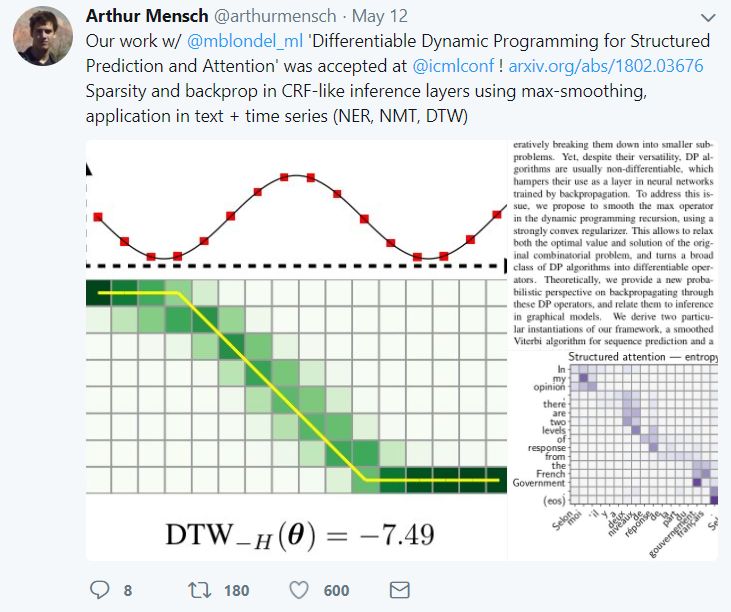
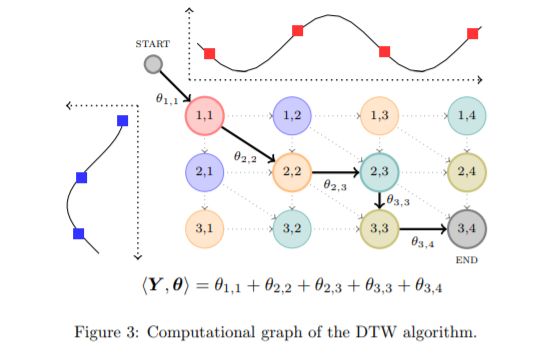
最热的就是这篇Arthur Mensch,来自法国Inria Parietal,scikit-learn 作者之一,关于结构性预测与注意力中的可微分动态编程。
作者重点指出:Sparsity and backprop in CRF-like inference layers using max-smoothing, application in text + time series (NER, NMT, DTW)。
Twitter上截止到现在 600赞。
论文网址:
http://www.zhuanzhi.ai/document/34c4176a60e002b524b56b5114db0e78
这位评价甚高! one of the most innovative deep learning papers!
欢迎大家阅读!
2. WaveRNN、Parralel WaveNet
来自DeepMind的两篇论文关于语音合成!
WaveRNN: http://arxiv.org/abs/1802.08435
Parallel WaveNet: http://arxiv.org/abs/1711.10433
WaveNet早已名声卓著,比原来快千倍,语音更自然,已经用在Google自家产品Google Assistant 里~
3. GAN性能表现分析
来自谷歌大脑GoodFellow团队,Is Generator Conditioning Causally Related to GAN Performance? find: 1. Spectrum of G's in/out Jacobian predicts Inception Score. 2. Intervening to change spectrum affects scores a lot
论文链接:https://t.co/cXQDEE2Uee
4.优化方法 Adam分析
Dissecting Adam: The Sign, Magnitude and Variance of Stochastic Gradients
论文地址:https://arxiv.org/abs/1705.07774
5. 图像转换器
论文地址:https://arxiv.org/abs/1802.05751
其他论文列表:
论文地址:Bayesian Quadrature for Multiple Related
Integrals https://arxiv.org/abs/1801.04153
Stein Points
https://arxiv.org/abs/1803.10161
Active Learning with Logged Data
https://arxiv.org/abs/1802.09069
Analyzing the Robustness of Nearest Neighbors to Adversarial Examples
https://arxiv.org/abs/1706.03922
Hierarchical Imitation and Reinforcement Learning
https://arxiv.org/abs/1803.00590
Analysis of Minimax Error Rate for Crowdsourcing and Its Application to Worker Clustering Model
https://arxiv.org/abs/1802.04551
Detecting and Correcting for Label Shift with Black Box Predictors
https://arxiv.org/abs/1802.03916
Yes, but Did It Work?: Evaluating Variational Inference
https://arxiv.org/abs/1802.02538
MAGAN: Aligning Biological Manifolds
https://arxiv.org/abs/1803.00385
Does Distributionally Robust Supervised Learning Give Robust Classifiers?
https://arxiv.org/abs/1611.02041
Knowledge Transfer with Jacobian Matching
https://arxiv.org/abs/1803.00443
Kronecker Recurrent Units
https://arxiv.org/abs/1705.10142
Entropy-SGD optimizes the prior of a PAC-Bayes bound: Generalization properties of Entropy-SGD and data-dependent priors
https://arxiv.org/abs/1712.09376
The Manifold Assumption and Defenses Against Adversarial Perturbations
https://arxiv.org/abs/1711.08001
Overcoming catastrophic forgetting with hard attention to the task
https://arxiv.org/abs/1801.01423
On the Opportunities and Pitfalls of Nesting Monte Carlo Estimators
https://arxiv.org/abs/1709.06181
Tighter Variational Bounds are Not Necessarily Better
https://arxiv.org/abs/1802.04537
LaVAN: Localized and Visible Adversarial Noise
https://arxiv.org/abs/1801.02608
Extracting Automata from Recurrent Neural Networks Using Queries and Counterexamples
https://arxiv.org/abs/1711.09576
Geometry Score: A Method For Comparing Generative Adversarial Networks
https://arxiv.org/abs/1802.02664
更多最新论文,请关注专知!获取更多AI知识信息资料,加入专知AI会员计划,学习、讨论、交流、合作:
点击上面图片加入会员
-END-
专 · 知
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请加专知小助手微信(扫一扫如下二维码添加),加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
请关注专知公众号,获取人工智能的专业知识!
点击“阅读原文”,使用专知