【GAN货】生成式对抗网络资料荟萃(原理/教程/报告/论文/实战/资料库)
【导读】近日来,专知后台经常能收到热心用户的留言,希望我们能多多分享生成式对抗网络相关学习资料。为此,专知内容小组特地为大家准备了GAN货合集大礼包,文中涵盖综述、论文、教程、代码、应用、调参等全链路学习内容,帮你一文看懂生成式对抗网络。此外,我们也提供本文pdf下载链接,请文章末尾查看。
简介
生成式对抗网络,是近些年来最火的无监督学习方法之一,模型由Goodfellow等人在2014年首次提出,将博弈论中非零和博弈思想与生成模型结合在一起,巧妙避开了传统生成模型中概率密度估计困难等问题,是生成模型达到良好的效果。
基本思想
囚徒困境
1950年,由就职于兰德公司的梅里尔·弗勒德和梅尔文·德雷希尔拟定出相关困境的理论,后来由顾问艾伯特·塔克以囚徒方式阐述,并命名为“囚徒困境”。经典的囚徒困境如下:
警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人有罪。于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择:
若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。
若二人都保持沉默(相关术语称互相“合作”),则二人同样判监半年。
若二人都互相检举(互相“背叛”),则二人同样判监5年。
纳什均衡
如同博弈论的其他例证,囚徒困境假定每个参与者(即“囚徒”)都是利己的,即都寻求最大自身利益,而不关心另一参与者的利益。那么囚徒到底应该选择哪一项策略,才能将自己个人的刑期缩至最短?两名囚徒由于隔绝监禁,并不知道对方选择;而即使他们能交谈,还是未必能够尽信对方不会反口。就个人的理性选择而言,检举背叛对方所得刑期,总比沉默要来得低。试设想困境中两名理性囚徒会如何作出选择:
若对方沉默、我背叛会让我获释,所以会选择背叛。
若对方背叛指控我,我也要指控对方才能得到较低的刑期,所以也是会选择背叛。
二人面对的情况一样,所以二人的理性思考都会得出相同的结论——选择背叛。背叛是两种策略之中的支配性策略。因此,这场博弈中唯一可能达到的纳什均衡,就是双方参与者都背叛对方,结果二人同样服刑5年。 这场博弈的纳什均衡,显然不是顾及团体利益的帕累托最优解决方案。以全体利益而言,如果两个参与者都合作保持沉默,两人都只会被判刑半年,总体利益更高,结果也比两人背叛对方、判刑5年的情况较佳。但根据以上假设,二人均为理性的个人,且只追求自己个人利益。均衡状况会是两个囚徒都选择背叛,结果二人判监均比合作为高,总体利益较合作为低。这就是“困境”所在。例子有效地证明了:非零和博弈中,帕累托最优和纳什均衡是互相冲突的。
生成模型与判别模型
机器学习的任务就是学习一个模型,应用这个模型,对给定的输入预测相应的输出。这个模型的一般形式为决策函数
判别方法由数据直接学习决策函数 f(X),或者条件概率分布 P(Y|X)作为预测模型,即判别模型。 生成方法由数据学习联合分布 P(X,Y),然后求出条件概率分布 P(Y|X)做预测的模型,即为生成模型,具体公式如下: P(Y|X)=P(X,Y)P(X)
相比于判别方法,生成模型更关注数据之间的内在联系,需要学习联合分布;而判别模型更关注于给定输入
生成式对抗网络
什么是对抗生成网络?用Ian Goodfellow自己的话来说:
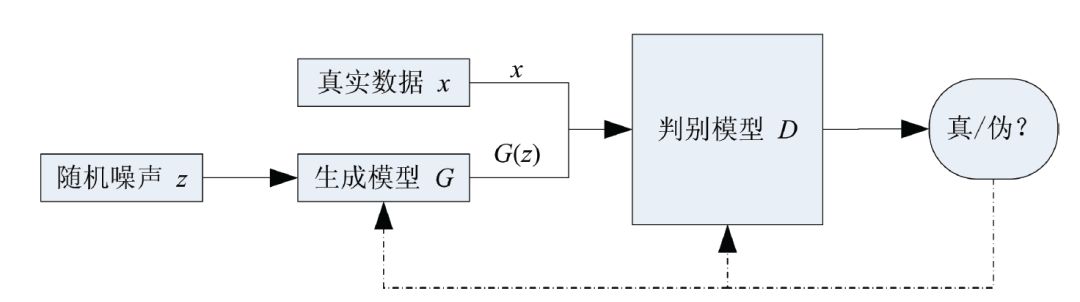
生成对抗网络是一种生成模型(Generative Model),其背后基本思想是从训练库里获取很多训练样本,从而学习这些训练案例生成的概率分布。而实现的方法,是让两个网络相互竞争,‘玩一个游戏’。其中一个叫做生成器网络( Generator Network),它不断捕捉训练库里真实图片的概率分布,将输入的随机噪声(Random Noise)转变成新的样本(也就是假数据)。另一个叫做判别器网络(Discriminator Network),它可以同时观察真实和假造的数据,判断这个数据到底是不是真的。”
基本原理
生成对抗网络是一个强大的基于博弈论的生成模型学习框架。该模型由GoodFellow在2014年首次提出,结合了生成模型和对抗学习思想。生成对抗网络的目的是训练一个生成模型 G,给定随机噪声向量noise,生成符合真实数据分布的样本。 G训练信号来自于判别器 D(x)。 D(x)的学习目标目是准确区分输入样本的来源(真实数据或生成数据), 而生成器 D的学习目标是生成尽可能真实的数据,使得判别器 G认为生成数据是真实的。整个模型使用梯度下降法进行训练,生成器和判别器可以根据特定的任务选择具体的模型,包括但不限于全连接神经网络(FCN)、卷积神经网络(CNN)、回归神经网络(RNN)、长短期记忆模型(LSTM)等。
基础知识
台大李弘毅老师gan课程。参考链接:
#youtube#:
https://www.youtube.com/watch?v=DQNNMiAP5lw&index=1&list=PLJV_el3uVTsMq6JEFPW35BCiOQTsoqwNw]
#bilibili#
https://www.bilibili.com/video/av24011528?from=search&seid=11459671583323410876]
成对抗网络初学入门:一文读懂GAN的基本原理
[http://www.xtecher.com/Xfeature/view?aid=7496]
深入浅出:GAN原理与应用入门介绍
[https://zhuanlan.zhihu.com/p/28731033]
港理工在读博士李嫣然深入浅出GAN之应用篇
[https://pan.baidu.com/s/1o8n4UDk] 密码: 78wt萌物生成器:如何使用四种GAN制造猫图
[https://zhuanlan.zhihu.com/p/27769807]GAN学习指南:从原理入门到制作生成Demo
[https://zhuanlan.zhihu.com/p/24767059x]生成式对抗网络GAN研究进展
[http://blog.csdn.net/solomon1558/article/details/52537114]
报告教程
NIPS 2016教程:生成对抗网络
[https://arxiv.org/pdf/1701.00160.pdf]
训练GANs的技巧和窍门
[https://github.com/soumith/ganhacks]OpenAI生成模型
[https://blog.openai.com/generative-models/]
论文前沿
对抗实例的解释和利用(Explaining and Harnessing Adversarial Examples)2014
[https://arxiv.org/pdf/1412.6572.pdf]基于深度生成模型的半监督学习( Semi-Supervised Learning with Deep Generative Models )2014
[https://arxiv.org/pdf/1406.5298v2.pdf]条件生成对抗网络(Conditional Generative Adversarial Nets)2014
[https://arxiv.org/pdf/1411.1784v1.pdf]基于深度卷积生成对抗网络的无监督学习(Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks (DCGANs))2015
[https://arxiv.org/pdf/1511.06434v2.pdf]基于拉普拉斯金字塔生成式对抗网络的深度图像生成模型(Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks)2015
[http://papers.nips.cc/paper/5773-deep-generative-image-models-using-a-5. laplacian-pyramid-of-adversarial-networks.pdf]生成式矩匹配网络(Generative Moment Matching Networks)2015
[http://proceedings.mlr.press/v37/li15.pdf]超越均方误差的深度多尺度视频预测(Deep multi-scale video prediction beyond mean square error)2015
[https://arxiv.org/pdf/1511.05440.pdf]通过学习相似性度量的超像素自编码(Autoencoding beyond pixels using a learned similarity metric)2015
[https://arxiv.org/pdf/1512.09300.pdf]对抗自编码(Adversarial Autoencoders)2015
[https://arxiv.org/pdf/1511.05644.pdf]基于像素卷积神经网络的条件生成图片(Conditional Image Generation with PixelCNN Decoders)2015
[https://arxiv.org/pdf/1606.05328.pdf]通过平均差异最大优化训练生成神经网络(Training generative neural networks via Maximum Mean Discrepancy optimization)2015
[https://arxiv.org/pdf/1505.03906.pdf]训练GANs的一些技巧(Improved Techniques for Training GANs)2016
[https://arxiv.org/pdf/1606.03498v1.pdf]
InfoGAN:基于信息最大化GANs的可解释表达学习(InfoGAN:Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets)2016
[https://arxiv.org/pdf/1606.03657v1.pdf]上下文像素编码:通过修复进行特征学习(Context Encoders: Feature Learning by Inpainting)2016
[http://www.cvfoundation.org/openaccess/content_cvpr_2016/papers/Pathak_Context_Encoders_Feature_CVPR_2016_paper.pdf]
生成对抗网络实现文本合成图像(Generative Adversarial Text to Image Synthesis)2016
[http://proceedings.mlr.press/v48/reed16.pdf]对抗特征学习(Adversarial Feature Learning)2016
[https://arxiv.org/pdf/1605.09782.pdf]结合逆自回归流的变分推理(Improving Variational Inference with Inverse Autoregressive Flow )2016
[https://papers.nips.cc/paper/6581-improving-variational-autoencoders-with-inverse-autoregressive-flow.pdf]深度学习系统对抗样本黑盒攻击(Practical Black-Box Attacks against Deep Learning Systems using Adversarial Examples)2016
[https://arxiv.org/pdf/1602.02697.pdf]参加,推断,重复:基于生成模型的快速场景理解(Attend, infer, repeat: Fast scene understanding with generative models)2016
[https://arxiv.org/pdf/1603.08575.pdf]f-GAN: 使用变分散度最小化训练生成神经采样器(f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization )2016
[http://papers.nips.cc/paper/6066-tagger-deep-unsupervised-perceptual-grouping.pdf]在自然图像流形上的生成视觉操作(Generative Visual Manipulation on the Natural Image Manifold)2016
[https://arxiv.org/pdf/1609.03552.pdf]对抗性推断学习(Adversarially Learned Inference)2016
[https://arxiv.org/pdf/1606.00704.pdf]基于循环对抗网络的图像生成(Generating images with recurrent adversarial networks)2016
[https://arxiv.org/pdf/1602.05110.pdf]生成对抗模仿学习(Generative Adversarial Imitation Learning)2016
[http://papers.nips.cc/paper/6391-generative-adversarial-imitation-learning.pdf]基于3D生成对抗模型学习物体形状的概率隐空间(Learning a Probabilistic Latent Space of Object Shapes via 3D Generative-Adversarial Modeling)2016
[https://arxiv.org/pdf/1610.07584.pdf]学习画画(Learning What and Where to Draw)2016
[https://arxiv.org/pdf/1610.02454v1.pdf]基于辅助分类器GANs的条件图像合成(Conditional Image Synthesis with Auxiliary Classifier GANs)2016
[https://arxiv.org/pdf/1610.09585.pdf]隐生成模型的学习(Learning in Implicit Generative Models)2016
[https://arxiv.org/pdf/1610.03483.pdf]VIME: 变分信息最大化探索(VIME: Variational Information Maximizing Exploration)2016
[http://papers.nips.cc/paper/6591-vime-variational-information-maximizing-exploration.pdf]生成对抗网络的展开(Unrolled Generative Adversarial Networks)2016
[https://arxiv.org/pdf/1611.02163.pdf]基于内省对抗网络的神经图像编辑(Neural Photo Editing with Introspective Adversarial Networks)2016,原文链接:
[https://arxiv.org/pdf/1609.07093.pdf]
基于解码器的生成模型的定量分析(On the Quantitative Analysis of Decoder-Based Generative Models )2016,原文链接:
[https://arxiv.org/pdf/1611.04273.pdf]
结合生成对抗网络和Actor-Critic 方法(Connecting Generative Adversarial Networks and Actor-Critic Methods)2016,原文链接:
[https://arxiv.org/pdf/1610.01945.pdf]
通过对抗网络使用模拟和非监督图像训练( Learning from Simulated and Unsupervised Images through Adversarial Training)2016,原文链接:
[https://arxiv.org/pdf/1612.07828.pdf]
基于上下文RNN-GANs的抽象推理图的生成(Contextual RNN-GANs for Abstract Reasoning Diagram Generation)2016,原文链接:
[https://arxiv.org/pdf/1609.09444.pdf]
生成多对抗网络(Generative Multi-Adversarial Networks)2016,原文链接:
[https://arxiv.org/pdf/1611.01673.pdf]
生成对抗网络组合(Ensembles of Generative Adversarial Network)2016,原文链接:
[https://arxiv.org/pdf/1612.00991.pdf]
改进生成器目标的GANs(Improved generator objectives for GANs) 2016,原文链接:
[https://arxiv.org/pdf/1612.02780.pdf]
训练生成对抗网络的基本方法(Towards Principled Methods for Training Generative Adversarial Networks)2017,原文链接:
[https://arxiv.org/pdf/1701.04862.pdf]
生成对抗模型的隐向量精准修复(Precise Recovery of Latent Vectors from Generative Adversarial Networks)2017,原文链接:
[https://openreview.NET/pdf?id=HJC88BzFl]
生成混合模型(Generative Mixture of Networks)2017,原文链接:
[https://arxiv.org/pdf/1702.03307.pdf]
记忆生成时空模型(Generative Temporal Models with Memory)2017,原文链接:
[https://arxiv.org/pdf/1702.04649.pdf]
AdaGAN: Boosting Generative Models". AdaGAN。原文链接[https://arxiv.org/abs/1701.04862]
Loss-Sensitive Generative Adversarial Networks on Lipschitz Densities。原文链接:[https://arxiv.org/abs/1701.06264];代码:[https://github.com/guojunq/glsgan/]
Wasserstein GAN, WGAN。原文链接:[https://arxiv.org/abs/1701.07875];代码:
[https://github.com/martinarjovsky/WassersteinGAN]
Boundary-Seeking Generative Adversarial Networks,BSGAN。原文链接:[https://arxiv.org/abs/1702.08431];代码地址:
[https://github.com/wiseodd/generative-models]
Generative Adversarial Nets with Labeled Data by Activation Maximization,AMGAN。原文链接:
[https://arxiv.org/abs/1703.02000]
Triple Generative Adversarial Nets,Triple-GAN。原文链接
[https://arxiv.org/abs/1703.02291]
BEGAN: Boundary Equilibrium Generative Adversarial Networks。原文链接:[https://arxiv.org/abs/1703.10717];代码:
[https://github.com/wiseodd/generative-models]
Improved Training of Wasserstein GANs。原文链接:[https://arxiv.org/abs/1704.00028];代码:
[https://github.com/wiseodd/generative-models]
MAGAN: Margin Adaptation for Generative Adversarial Networks。原文链接[https://arxiv.org/abs/1704.03817],
代码:
[https://github.com/wiseodd/generative-models]
Gang of GANs: Generative Adversarial Networks with Maximum Margin Ranking。原文链接:
[https://arxiv.org/abs/1704.04865]
Softmax GAN。原文链接:
[https://arxiv.org/abs/1704.06191]
Generative Adversarial Trainer: Defense to Adversarial Perturbations with GAN。原文链接:
[https://arxiv.org/abs/1705.03387]
Flow-GAN: Bridging implicit and prescribed learning in generative models。原文链接:
[https://arxiv.org/abs/1705.08868]
Approximation and Convergence Properties of Generative Adversarial Learning。原文链接:
[https://arxiv.org/abs/1705.08991]
Towards Consistency of Adversarial Training for Generative Models。原文链接:
[https://arxiv.org/abs/1705.09199]
Good Semi-supervised Learning that Requires a Bad GAN。原文链接:[https://arxiv.org/abs/1705.09783]
On Unifying Deep Generative Models。原文链接:
[https://arxiv.org/abs/1706.00550]
DeLiGAN:Generative Adversarial Networks for Diverse and Limited Data。原文链接:
[http://10.254.1.82/cache/6/03/openaccess.thecvf.com/e029768353404049dbcac9187a363d5a/Gurumurthy_DeLiGAN__Generative_CVPR_2017_paper.pdf];代码:[https://github.com/val-iisc/deligan]
Temporal Generative Adversarial Nets With Singular Value Clipping。原始链接:
[http://openaccess.thecvf.com/content_ICCV_2017/papers/Saito_Temporal_Generative_Adversarial_ICCV_2017_paper.pdf]
Least Squares Generative Adversarial Networks. LSGAN。原始链接:
[http://openaccess.thecvf.com/content_ICCV_2017/papers/Mao_Least_Squares_Generative_ICCV_2017_paper.pdf]
工程实践
深度卷积生成对抗模型(DCGAN)参考链接
[https://github.com/Newmu/dcgan_code]
用Keras实现MNIST生成对抗模型,参考链接:
[https://oshearesearch.com/index.PHP/2016/07/01/mnist-generative-adversarial-model-in-keras/]
用深度学习TensorFlow实现图像修复,参考链接:
[http://bamos.github.io/2016/08/09/deep-completion/]
TensorFlow实现深度卷积生成对抗模型(DCGAN),参考链接:
[https://github.com/carpedm20/DCGAN-tensorflow]
Torch实现深度卷积生成对抗模型(DCGAN),参考链接:
[https://github.com/soumith/dcgan.torch]
Keras实现深度卷积生成对抗模型(DCGAN),参考链接:
[https://github.com/jacobgil/keras-dcgan]
使用神经网络生成自然图像(Facebook的Eyescream项目),参考链接:
[https://github.com/facebook/eyescream]
对抗自编码(AdversarialAutoEncoder),参考链接:
[https://github.com/musyoku/adversarial-autoencoder]
利用ThoughtVectors 实现文本到图像的合成,参考链接:
[https://github.com/paarthneekhara/text-to-image]
对抗样本生成器(Adversarialexample generator),参考链接:
[https://github.com/e-lab/torch-toolbox/tree/master/Adversarial]
深度生成模型的半监督学习,参考链接:
[https://github.com/dpkingma/nips14-ssl]
GANs的训练方法,参考链接:
[https://github.com/openai/improved-gan]
生成式矩匹配网络(Generative Moment Matching Networks, GMMNs),参考链接:
[https://github.com/yujiali/gmmn]
对抗视频生成,参考链接:
[https://github.com/dyelax/Adversarial_Video_Generation]
基于条件对抗网络的图像到图像翻译(pix2pix)参考链接:
[https://github.com/phillipi/pix2pix]
对抗机器学习库Cleverhans, 参考链接:
[https://github.com/openai/cleverhans]
资料收集
生成对抗网络(GAN)专知荟萃。参考资料:
[http://www.zhuanzhi.ai/topic/2001150162715950/awesome]
The GAN Zoo千奇百怪的生成对抗网络,都在这里了。你没看错,里面已经有有近百个了。参考链接:
[https://github.com/hindupuravinash/the-gan-zoo]
gan资料集锦。参考链接:
[https://github.com/nightrome/really-awesome-gan]
gan在医学上的案例集锦:
[https://github.com/xinario/awesome-gan-for-medical-imaging]
gan应用集锦:
[https://github.com/nashory/gans-awesome-applications]
生成对抗网络(GAN)的前沿进展(论文、报告、框架和Github资源)汇总,参考链接:
[http://blog.csdn.net/love666666shen/article/details/74953970]
请关注专知公众号(扫一扫最下面专知二维码,或者点击上方蓝色专知),
后台回复“GAN3” 就可以获取全文PDF下载链接~
-END-
专 · 知
人工智能领域26个主题知识资料全集获取与加入专知人工智能服务群: 欢迎微信扫一扫加入专知人工智能知识星球群,获取专业知识教程视频资料和与专家交流咨询!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请加专知小助手微信(扫一扫如下二维码添加),加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
请关注专知公众号,获取人工智能的专业知识!
点击“阅读原文”,使用专知