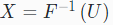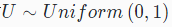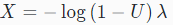【深度干货】专知主题链路知识推荐#5-机器学习中似懂非懂的马尔科夫链蒙特卡洛采样（MCMC）入门教程01- 专知

【深度干货】专知主题链路知识推荐#5-机器学习中似懂非懂的马尔科夫链蒙特卡洛采样（MCMC）入门教程01

【导读】主题链路知识是我们专知的核心功能之一，为用户提供AI领域系统性的知识学习服务，一站式学习人工智能的知识，包含人工智能（机器学习、自然语言处理、计算机视觉等）、大数据、编程语言、系统架构。使用请访问专知进行主题搜索查看 - 桌面电脑访问www.zhuanzhi.ai, 手机端访问www.zhuanzhi.ai 或关注微信公众号后台回复" 专知"进入专知，搜索主题查看。今天给大家继续介绍我们独家整理的机器学习——马尔科夫链蒙特卡洛采样（MCMC）方法。

上一次我们详细介绍了贝叶斯参数估计，里面我们说过贝叶斯估计的时候，有时候未知参数的其后验分布多为高维、复杂的非常见分布，对这些高维积分进行计算十分困难，这一困难使得贝叶斯推断方法在实践中的应用受到很大的限制，在很长一段时间，贝叶斯推断主要用于处理简单低维的问题，以避免计算上的困难，比如LDA中隐变量的后验分布就比较复杂。目前机器学习中有好多方法可以解决，比如使用变分推断或者采样的方式模拟这个分布等等，今天我们详细介绍马尔科夫链蒙特卡洛采样（MCMC）方法入门教程，计划分两次更新，今天先介绍使用比较简单的方法来对基本的分布进行采样——从随机变量分布中采样。

一直想把马尔科夫链蒙特卡洛采样的详细过程总结并写出来，尽管网上的中文教材比较多，但暂时没有发现写的比较浅显易懂并且条理分明的博客文章，偶然间看到这个英文教程，清晰地记得那时候花一天时间通读全文，并且代码跑通实现了，很多以前似懂非懂的采样问题突然清晰明白了，现在花时间整理，并且把英文教程前两章翻译出来，希望对大家有用，有问题或者理解有偏差的地方，欢迎指出来，一起学习进步。

1、从随机变量分布中采样

研究人员提出的概率模型对于分析方法来说往往过于复杂。越来越多的研究人员依赖数学计算的方法处理复杂的概率模型，研究者通过使用计算的方法，摆脱一些分析技术所需要的不切实际的假设。（如，正态和独立）

大多数近似方法的关键是在于从分布中采样的能力，我们需要通过采样来预测特定的模型在某些情况下的行为，并为潜在的变量（参数）找到合适的值以及将模型应用到实验数据中，大多数采样方法都是将复杂的分布中抽样的问题转化到简单子问题的采样分布中。

本章，我们解释两种采样方法：逆变换方法（the inverse transformation method）和拒绝采样（rejection sampling）。这些方法主要适用于单变量的情况，用于处理输出单变量的问题。在下一章，我们讨论马尔科夫链蒙特卡洛方法（Markov chain Monte Carlo），该方法可以有效的用于多元变量分布采样。

1.1 标准分布

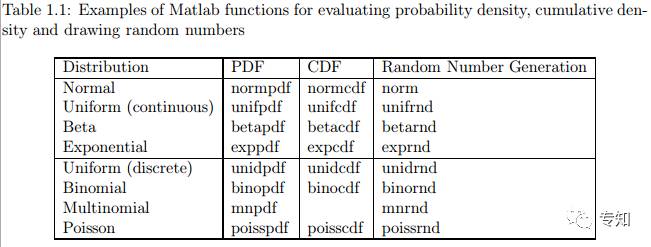
有一些分布被经常用到，这些分布被MATLAB作为标准分布实现。在MATLAB统计工具箱（Matlab Statistics Toolbox supports）实现了一系列概率分布。使用MATLAB工具箱可以很方便的计算这些分布的概率密度、累积密度、并从这些分布中取样随机值。表1.1列举了一些MATLAB工具箱中的标准分布。在MATLAB文档中列举了更多的分布，这些分布可以用MATLAB模拟。利用在线资源，通常很容易能找到对其他常见分布的支持。

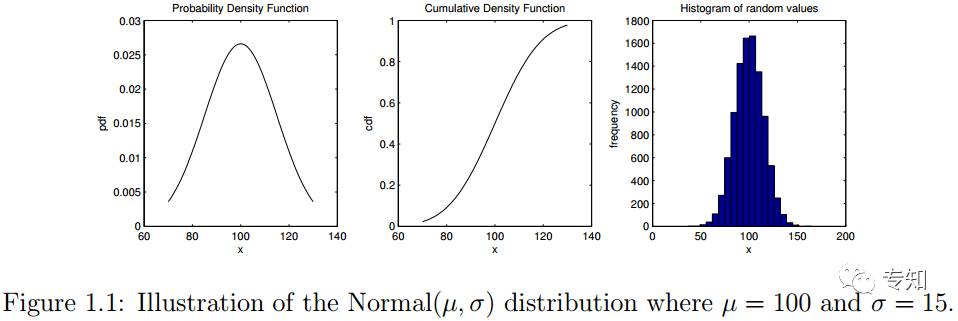
为了说明如何使用这些函数，Listing 1.1展示了正态分布N(μ,σ)可视化的MATLAB代码，其中μ=100,σ=15。

举例

举个例子，可以想象一下用该正态分布表示观察到的人群的IQ系数变化。该代码显示了了如何展示概率密度和累积密度。它还展示了如何从该分布中抽取随机值以及如何使用hist函数可视化这些随机样本。代码的输出结果如图1.1所示。类似的，图1.2可视化离散的二项分布Binomial(N,θ)，其中参数N=10,θ=0.7。该分布可认为是进行10次实验，每次试验成功的概率是θ=0.7。（所有代码见最后百度云链接）

1 %% Explore the Normal distribution N( mu , sigma ) 2 mu = 100; % the mean 3 sigma = 15; % the standard deviation 4 xmin = 70; % minimum x value for pdf and cdf plot 5 xmax = 130; % maximum x value for pdf and cdf plot 6 n = 100; % number of points on pdf and cdf plot 7 k = 10000; % number of random draws for histogram 8 9 % create a set of values ranging from xmin to xmax 10 x = linspace( xmin , xmax , n ); 11 p = normpdf( x , mu , sigma ); % calculate the pdf 12 c = normcdf( x , mu , sigma ); % calculate the cdf 13 14 figure( 1 ); clf; % create a new figure and clear the contents 15 16 subplot( 1,3,1 ); 17 plot( x , p , 'k−' ); 18 xlabel( 'x' ); ylabel( 'pdf' ); 19 title( 'Probability Density Function' ); 20 21 subplot( 1,3,2 ); 22 plot( x , c , 'k−' ); 23 xlabel( 'x' ); ylabel( 'cdf' ); 24 title( 'Cumulative Density Function' ); 25 26 % draw k random numbers from a N( mu , sigma ) distribution 27 y = normrnd( mu , sigma , k , 1 ); 28 29 subplot( 1,3,3 ); 30 hist( y , 20 ); 31 xlabel( 'x' ); ylabel( 'frequency' ); 32 title( 'Histogram of random values' );

Listing 1.1: Matlab code to visualize Normal distribution.

1.2 从非标准分布中采样

我们希望MATLAB工具也支持从非标准分布中采样，这种情况在建模过程中经常出现，因为研究人员可以提出一种新的噪声过程或已存在分布的组合方式。复杂采样问题的计算方法通常依赖于我们已经知道如何有效地进行采样的分布。这些从简单分布中采样的随机值可以被转换成目标分布需要的值。事实上，这一节我们讨论的一些技术是MATLAB的内部分布，如正态分布和指数分布。

1.2.1 用离散变量进行逆变换采样（Inverse transform sampling）

逆变换采样（也被成为逆变换方法）即给定累积分布函数的逆，可从任意概率分布中生成随机数。这个方法是对均匀分布的随机数字进行采样（在0到1之间）然后使用逆累积分布函数转换这些值。该过程的简单之处就在于，潜在的采样仅仅依赖对统一的参数进行偏移和变换。该过程可以用于采样很多不同种类的分布，事实上，MATLAB实现很多随机变量生成方法也是基于该方法的。

在离散分布中，我们知道每个输出结果的概率。这种情况下，逆变换方法就需要一个简单的查找表。

给定一个非标准的离散分布的例子，我们使用一些实验数据来研究人类如何能产生一致的随机数（如Treisman and Faulkner,1987）。在这些实验中，被测试者会产生大量的随机数字（0,…,9）。研究人员根据每个随机数字的相对频率进行制表。你可能会怀疑实验对象不会总是产生均匀分布。表1.2.1展示了一些典型的数据，其中可以看出一些比较低的和高的数字容易被忽视，而一些特殊数字（如数字4）占过高的比例。由于某种原因，数字0和9从来没有被产生。在任何情况下，这些数字都是相当典型的，而且证明了人类不能很好地产生均匀分布的随机数字。

假设我们想要模拟这个过程，并根据表1.2.1中的概率编写一个算法采样数字。因此，程序应该用概率0.2生成数字4，根据概率0.175生成数字5等。例如，Listing1.2中的代码使用MATLAB内置的函数randsample来实现这个过程。代码的输出结果如图1.2.1所示。

1 % Simulate the distribution observed in the 2 % human random digit generation task 3 4 % probabilities for each digit 5 theta = [0.000; ... % digit 0 6 0.100; ... % digit 1 7 0.090; ... % digit 2 8 0.095; ... % digit 3 9 0.200; ... % digit 4 10 0.175; ... % digit 5 11 0.190; ... % digit 6 12 0.050; ... % digit 7 13 0.100; ... % digit 8 14 0.000 ] ... % digit 9 15 16 % fix the random number generator 17 seed = 1; rand( 'state' , seed ); 18 19 % let's say we draw K random values 20 K = 10000; 21 digitset = 0:9; 22 Y = randsample(digitset,K,true,theta); 24 % create a new figure 25 figure( 1 ); clf; 26 27 % Show the histogram of the simulated draws 28 counts = hist( Y , digitset ); 29 bar( digitset , counts , 'k' ); 30 xlim( [ −0.5 9.5 ] ); 31 xlabel( 'Digit' ); 32 ylabel( 'Frequency' ); 33 title( 'Distribution of simulated draws of human digit generator' );

Listing 1.2: Matlab code to simulate sampling of random digits.

Figure 1.2.1: Illustration of the inverse transform procedure for generating discrete random variables. Note that we plot the cumulative probabilities for each outcome. If we sample a uniform random number of U = 0.8, then this yields a random value of X = 6

如果不采用内置的函数如randsample 和mnrnd，而是通过逆变换方法来实现底层的采样算法对我们更有帮助。我们首先需要计算累计概率分布，换句话说，我们需要知道我们观察到的结果等于或小于某一特定值的概率。如果F(X)表示累计函数，我们需要计算F(X=x)=p(X≤x)。对于离散分布，计算这个值可以通过简单的求和。我们的例子的累计概率在表1.2.1的最后一列中给出。在逆变换算法中，该想法是采样随机偏差（0和1之间的随机数）并将随机数与表中的累计概率比较。随机偏差的第一个结果小于（或等于）相关的累计概率与抽样结果相对应。图1.2.1展示了一个例子，其中随机偏差U=0.8，导致采样结果X=6。这个重复采样随机偏差的过程，并与累积分布相比较，就会形成离散变量的逆变换方法的基础。注意我们应用了一个逆函数，因为做的是逆表的查找。

1.2.2 连续变量的逆变换采样

逆变换样方法也可以用于连续分布。一般地，该方法目的是获得均匀的随机偏差并且将逆函数应用在随机偏差的累积分布中。下面，令F(X)是目标变量 X X的累积密度函数（cumulative density function，CDF），F−1(X)是该函数的逆。我们希望获得随机变量 X X的值，可以通过如下步骤获取：

获得均匀分布U∼Uniform(0,1)
设
重复上述采样过程

可通过一个简单的例子解释上述方法。假设我们要从指数分布（exponential distribution）中采样随机数。当λ>0时，累积密度函数是F(x∣λ)=1−exp(−x/λ)。用一些简单的代数方法，就可以求出这个函数的逆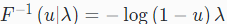。从而引出了下面的从Exponental(λ)分布中采样随机数的步骤：

获得均匀分布
设
重复上述采样过程

1.2.3 拒绝采样

在很多情况下，逆变换采样方法是不适用的，因为很难计算其累积分布和它的逆。在这种情况下，有其他的可供选择的采样方法，如拒绝采样，以及其他使用马尔科夫链蒙特卡洛的方法，将在下一章进行讨论。拒绝采样的主要优势在于它不需要“burn-in”过程。和其他方法相反，所有的样本在采样过程中获得，并且可直接作为目标分布的样本。

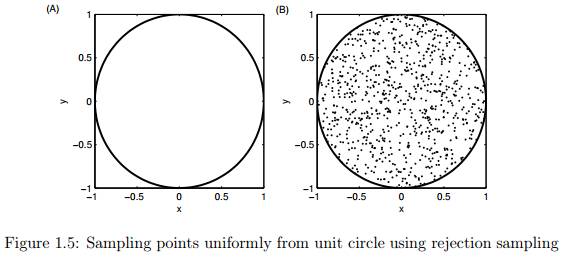
拒绝采样的一般概念可用图1.5进行解释。假设我们想在以(0,0)为圆心以1为半径的圆形内均匀画点。乍一看，似乎很难均匀地在这个圆内直接进行采样。但是我们可以应用拒绝采样的方法进行采样，首先确定圆外围的正方形，在正方形中采样(x,y)的值，剔除满足式子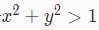的所有的取值。注意在这个过程中我们使用了一个简单的建议分布（q），如均匀分布，作为从更复杂的分布中采样的基础。

拒绝采样允许我们从难以采样的分布中生成样本，在这些难以采样的分布中我们可以计算任何特定样本的概率。换句话说，假定我们有一个分布p(θ)，并且难以直接从该分布中采样，但是我们可以计算其特定值的概率密度p(θ)。

第一件要做的就是建议分布（proposal distribution）。建议分布就是指一个简单的分布，记为q(θ)，该分布是可以直接进行采样的。主要思路是，计算同时满足建议分布和目标分布采样的概率，然后拒绝相对于建议分布中那些不太可能出现在目标分布下的样本。

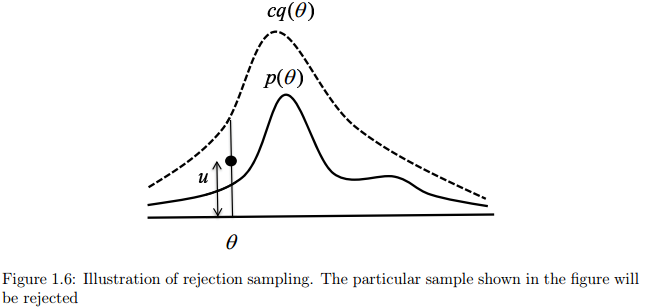
图1.6说明了这个过程。我们首先需要找到一个常量 c 使之对所有的可能的样本θ满足cq(θ)≥p(θ)。建议函数q(θ)乘以常量 c 被称为比较分布，并且使其总是大于目标分布。要确定常数 c c并不容易，我们先假定可以通过微积分确定该常数。

我们首先从均匀分布[0,cq(θ)]中获取一个数u，换句话说，这是直线段从0到cq(θ)的某个点以θ为建议的比较分布。如果u>p(θ)，我们拒绝这个建议分布采样得到的值，否则，接受之。如果接受了某个建议，则采样值θ就是从目标分布p(θ)中获得的。上述的采样过程步骤如下：

步骤

选择一个容易采样的分布q(θ)
确定常量c，使对所有θ的有cq(θ)≥p(θ)
从建议分布q(θ)中采样一个建议样本θ
从区间[0,cq(θ)]采样一个数u
如果u>p(θ)则拒绝，否则接受
重复步骤3,4,5，直到达到要求的样本数量；每个接受的样本都是从p(θ)中获得的

这种算法有效的关键就是需要有尽可能多的样本被接受，这取决于建议分布q(θ)的选择。建议分布不同于目标分布，它会导致很多拒绝接受的样本，这将减慢采样的速度。

后续介绍MCMC，敬请期待！

以上是MCMC内容的第一部分，有些名词或者语句由于时间原因有问题，请大家随时提出来，谢谢了。
代码链接： http://pan.baidu.com/s/1qXIWzJu

MCMC matlab tutorial 电子版本：http://pan.baidu.com/s/1i48vyr7

Reference

Mark Steyver. Computational Statistics with Matlab. 2011

欢迎大家使用专知！点击阅读原文即可访问，访问专知，搜索主题，获取更多关于马尔科夫链蒙特卡洛方法信息。

上面就是关于机器学习中马尔科夫链蒙特卡洛理论的一个总结，建议大家多多体会分布如何使用MCMC进行模拟，有什么问题可以在我们的专知公众号平台（桌面端或手机端直接访问 www.zhuanzhi.ai,一站式的AI知识服务）上交流或者加我们的专知-人工智能交流群 426491390

同时请，关注我们的公众号，获取最新关于专知以及人工智能的资讯、技术、算法等内容。扫一扫下方关注我们的微信公众号。

查看更多专知主题链路知识：

专知主题链路知识推荐#1——马尔科夫链蒙特卡洛采样(附代码)

专知主题链路知识推荐#2——参数估计方法

专知主题链路知识推荐#4-机器学习中往往被忽视的贝叶斯参数估计方法

专知主题链路知识推荐#5-机器学习算法-决策树完整学习教程

展开全文

阅读 1+

评论 0+