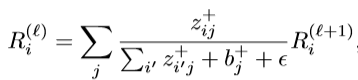【论文笔记】图卷积的解释性技术
【导读】本篇论文主要工作研究图卷积的解释性,使用基于梯度和基于分解的两种方法,为未来的发展奠定了基础。

Graph Network
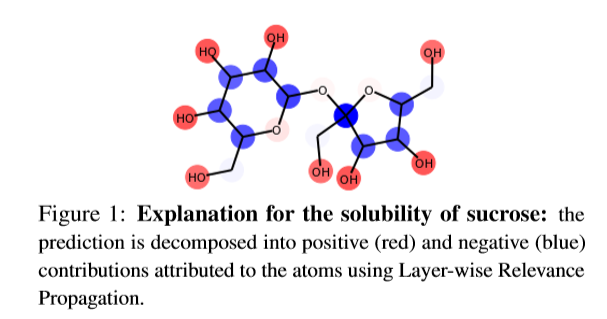
论文中提到了蔗糖的溶解图,且把该图假定为GNs的一般形式:
图可以包含边E={e_k},节点V={v_i}以及图级别u。在计算的每一层,图都使用三个更新函数φ和三个聚合函数φ进行更新:
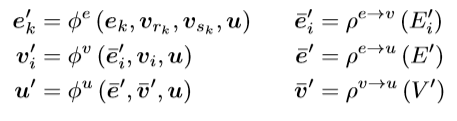
其中rk,sk表示第k个边的发送和接受节点, 集合E'_i, E', V '表示与节点i联的边,由\phi^e更新,所有节点由\phi^n更新,每个处理层都保持图的结构不变,只更新图的特征,而不更新其拓扑结构。映射f:(E,V,u)→y可以表示单个感兴趣的量(例如分子的溶解性)或具有对节点和边的单独预测的图。在这项工作中,所有的都是线性转换的,然后是ReLU激活,所有的转换都是sum/mean/max池操作。

Explainability
1)灵敏度分析(SA):利用梯度w.r.t的平方范数对可微函数f的预测产生局部解释,输入x:S(x) \propto ||\nabla_xf||^2,用这种方法生成的显著性图S描述了输入的变化会在多大程度上引起输出的变化。
2)引导式反向传播(GBP):利用梯度构建saliency map(Springenberg等人,2015年)。与SA不同的是,反向传播时会去掉负梯度。
3)层相关传播(LRP):通过将每个转换的输出信号分解为其输入的组合来生成相关图。对于某些权重和激活的配置,LRP可以解释为重复的泰勒分解。与前两种方法不同,LRP识别出输入的哪些特征对最终预测贡献最大,而不是关注其变化。此外,它还能够处理积极和消极的相关性,从而对影响因素进行更深入的分析。
(Bach等人,2015)介绍了LRP的两个规则,即\alpha \beta-规则和\epsilon稳定规则。
\alpha \beta-规则
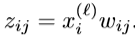
其中α+β=1,x是输入,w是它的权重。
\epsilon稳定规则
以上三种方法都依赖于通过网络的反向传递来传播输出的梯度/相关性,并将其累积到输入。由于GN的计算图可以变得复杂和非连续,因此我们利用pytorch的跟踪能力,在其autograd模块上实现这些算法。

讨论
通过本文所做的实验,我们希望突出图域的一些关键差异,这些差异需要特别考虑才能产生有意义的解释。
1)连接的作用
图像可以看作是具有规则网格拓扑结构的图形,对于具有不规则连通性的图,边获得了一个更突出的角色,当基于图像时时,这种角色可能会被忽略。例如,在边特征不存在或完全相同(不具有信息性)的图形中,即使两个节点之间的连接本身是一个信息源,也不会将梯度和相关性传播回这些连接,以便进行解释。我们建议利用图卷积的结构保持性在消息传递(message-passing)的多个步骤中聚合解释(aggregate explanations),认为连接的重要性应该从中间步骤中产生(如下图)。
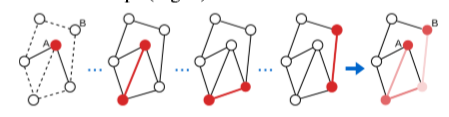
节点A预测节点B。即使输入图形在边缘上没有特征(表示为虚线),也通过聚合图卷积的多个步骤的相关性来识别相关路径A→B。
2)池化
Architectural choice : 在标准NN中,通常使用池化操作来聚合特征。在信息传递GNs中,池化用于在局部和全局级别聚合边缘和节点特征,而不修改网络的拓扑结构。GN中池化函数的选择与学习问题密切相关,例如,和池化(sum pooling)最适合在全局级别进行计数,而最大池化(max pooling)可用于标识局部属性。
Explanations:聚合的选择也影响为预测获得的解释。和池化和平均池化(Sum and mean pooling)将梯度/相关性传播到所有输入,可能识别所有信号源。相反,max pooling只考虑它的一个输入,而忽略其他输入,不管其大小,这可能导致不完整的解释(例如,多个相邻的生病节点可以解释一个感染节点)。为了解决这一问题,LRP建议在关联传播过程中用L_p范数来近似最大池化,但这种方法可能过度分散关联性(over-disperse)与不重要的输入。我们建议将后向传播(backward pass)通过最大池化作为一个搜索,只重新分配与这些输入的相关性,如果选择为最大值,则会导致类似的预测。
作者基于玩具图和化学回归问题来评价GNs的不同解释方法(SA、GBP、LRP)。

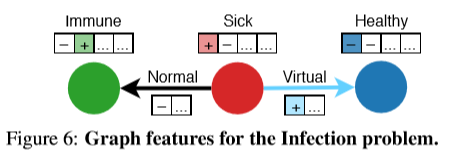
实验一:感染
在这个玩具图中,输入的图表示一组不同的人群,他们或是身体健康,或是身体欠安,亦或对某种疾病有免疫。人和人之间的有向线段代表他们之间的关系,特征是虚拟的还是非虚拟的。这种疾病按照一个简单的规则传播:患病节点(红色表示)通过非虚拟边感染与其相连的邻居,除非目标节点免疫(绿色表示)。其目标是为了预测传播之后每一节点的状态,然后根据logical infection dynamics评估SA、GB和LRP的正确性。当任务是解释单个节点的预测时,这三种技术都可以识别输入图的相关节点/边。然而,我们注意到,基于变量(variation-based)的方法产生的解释往往不同于人类如何直观地从因果角度(in terms of cause and effect)描述过程,而LRP结果更自然。
SA在节点本身上具有很高的相关性(如果节点2在开始时患病率更高,则在结束时感染率更高)。GBP正确地将节点1识别为感染源,但边的重要性很小。LRP将预测分解为负贡献(蓝色,节点2没有生病),两个正贡献(红色,节点1生病,1→2没有虚拟)。由于最大池化,节点4被忽略。
1)实验任务
经过训练,网络应该识别出感染节点(预测值为1),其他节点预测为0。并识别出被感染节点的邻居,连接类型以及免疫状态。网络还输出图标预测,该预测对应感染节点的总数。
2)实验细节
特征表示法
特征向量[e_k]∈[-1,+1]^2和n_i∈[-1,+1]^4,分别对边和节点特征进行编码。值得注意的是,二进制特征编码为{−1、+1}而不是{0,1},虽然这不会影响基于变量的模型(SA和GPB),但它有助于在使用LRP时传播与输入的相关性。用于训练的合成数据集包含100000个,其中30个或更少的节点由Barabasi-Albert算法生成。用于验证和测试的数据集包含多达60个节点的图以及疾病和免疫节点的不同百分比。
构架和训练
边和节点的更新函数是浅层多层感知器,带有ReLU激活,我们使用sum/max池化来聚合与节点相关的边。我们使用Adam优化器最小化每个节点预测和真实值(the ground truth)之间的二进制交叉熵。多个超参数的选择,如学习率、隐藏层中神经元的数量和L1的正则化产生了相似的结果。
节点编码它们是生病还是健康,是免疫还是有风险,加上两个非形成性特征。边缘编码,不管它们是否是虚拟的,加上一个单一的非格式化特征。

实验二:溶解性
我们训练一个GN,从分子图中预测有机化合物的水溶性(aqueous solubility of organic),我们的多层GN与它们的性能匹配,同时保持简单。
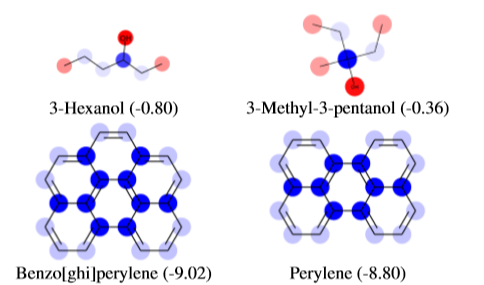
在解释网络预测时,LRP将正相关和负相关归因于已知与溶解性相关的特征,例如分子外部存在R-OH基团,以及通常表示低溶解性的特征,例如重复的非极性芳香环(如下图)。最初引入LRP是为了解释分类预测,但在这里它被用于回归任务。
1)实验任务
从有机分子的结构预测其水溶解度。
2)实验细节
数据集与功能
数据集源自(Duvenaud等人,2015年),大概有1000个有机分子组成,这些有机分子表示为Smiles字符串及其在水中的测量溶解性,分子表示为以原子为节点和以边为键的图。
构架和训练
使用测量的对数溶解度与多层gn输出图的全局特征u之间的均方误差作为优化目标。使用多层图卷积,网络可以以越来越大的尺度聚合信息,从局部邻域开始,并扩展到更广泛的原子群。

实验结果
1)感染
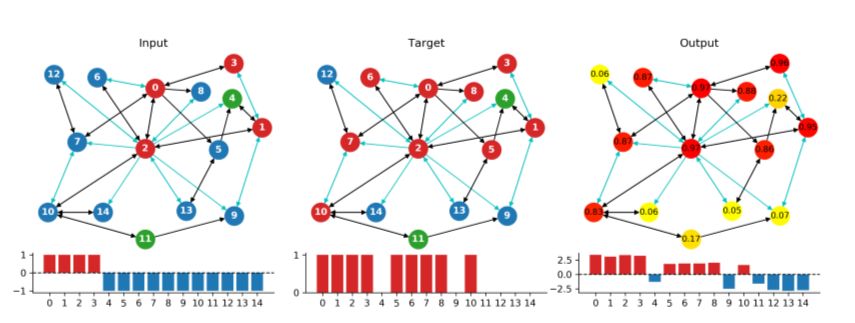
如图,实验中有多个感染源(节点0,1,2,3)和免疫节点(节点4,11),该网络使用最大池化聚合边缘信息,感染传播一步之后预测出节点的状态,如图,节点5,6,7,8,10为被传播感染节点。
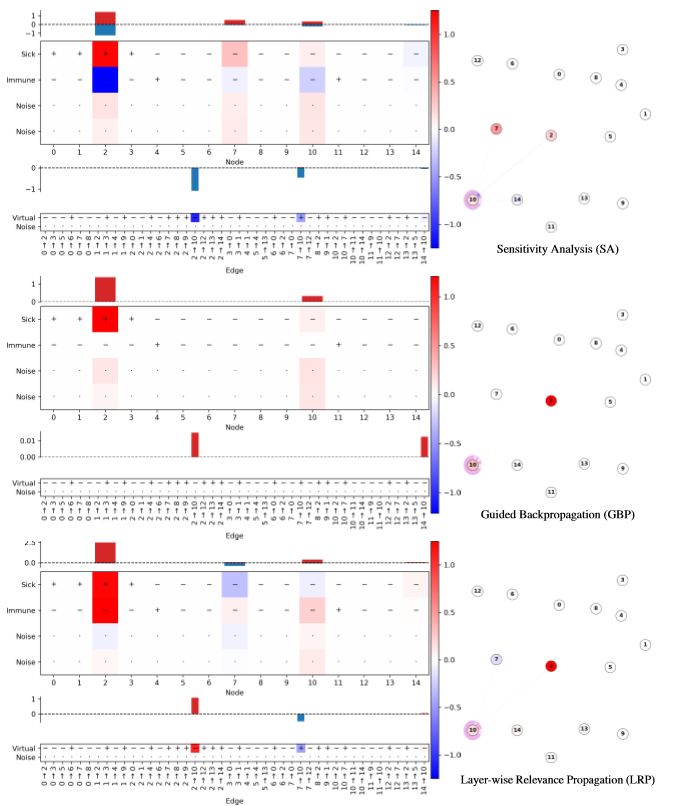
上图为3种不同方法来分析节点10受节点2,7,14以及边的影响。节点10最初的健康的,受到节点2的入侵(2->10非虚拟边)后,节点10病变。
2)溶解性
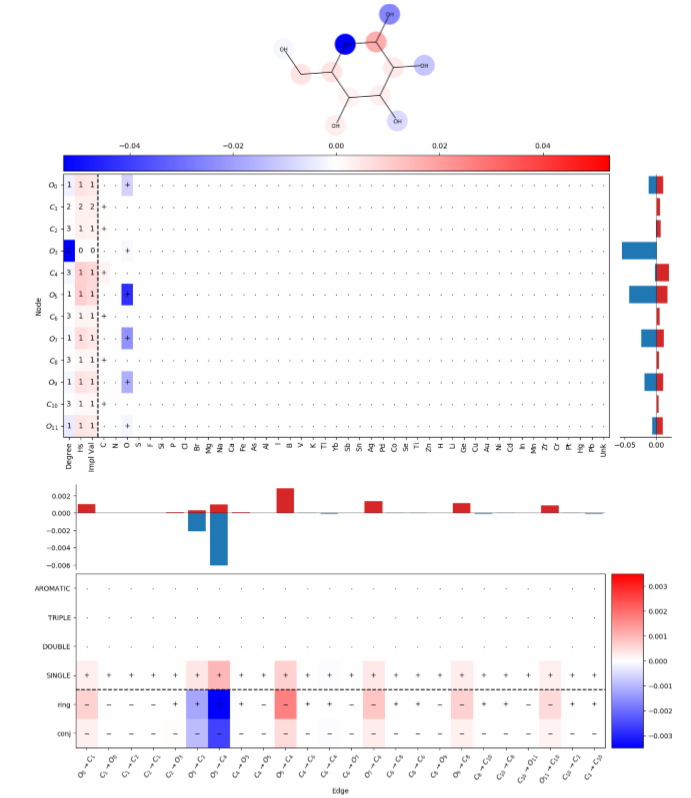
上图使用逐层相关性传播对原子和键特征进行解释。

代码复现
环境准备
Python3.7 ,pytorch1.1.0,作者提供该项目所需要的库,均放在conda.yaml中,因此可按着作者提示创建环境并安装所需的库:
conda env create -n gn-exp -f conda.yamlconda activate gn-exppython setup.py develop
实验一:感染
1)创建文件
INFECTION=~/experiments/infection/
mkdir -p "$INFECTION/"{runs,data}
2)创建数据集
python -m infection.dataset generate ../config/infection/datasets.yaml #此处填写完整的代码路径 "folder=${INFECTION}/data"
data文件生成以下三个文件:

python -m infection.dataset generate ../config/infection/datasets.yaml#此处填写完整的代码路径" folder=${INFECTION}/smalldata" datasets.{train,val}.num_samples=5000
注:代码中句子与句子之间有一个空格
3)训练
python -m infection.train --experiment ../config/infection/train.yaml --model ../config/count_nodes/minimal.yaml
源码中有一处错误,/infection/train.yaml中第15行改为:
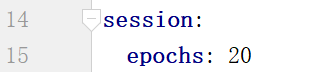
4)实验模型
继承nn.Model类,创建两层神经网络:
class MinimalGN(nn.Module): def __init__(self, in_node_features_shape, out_node_features_shape, out_global_features_shape): super().__init__() self.g_n = nn.Linear(in_node_features_shape, out_node_features_shape) self.h_n = nn.Linear(out_node_features_shape, out_global_features_shape)
实验二:溶解性
1)创建文件
SOLUBILITY=~/experiments/solubility/
mkdir -p "$SOLUBILITY/"{runs,data}
2)训练
python -m solubility.train --experiment ../config/solubility/train.yaml --model ../config/count_nodes/minimal.yaml
-END-
专 · 知
专知,专业可信的人工智能知识分发,让认知协作更快更好!欢迎登录www.zhuanzhi.ai,注册登录专知,获取更多AI知识资料!
欢迎微信扫一扫加入专知人工智能知识星球群,获取最新AI专业干货知识教程视频资料和与专家交流咨询!
请加专知小助手微信(扫一扫如下二维码添加),加入专知人工智能主题群,咨询技术商务合作~

专知《深度学习:算法到实战》课程全部完成!560+位同学在学习,现在报名,限时优惠!网易云课堂人工智能畅销榜首位!
点击“阅读原文”,了解报名专知《深度学习:算法到实战》课程