模型压缩究竟在做什么？我们真的需要模型压缩么？

【导读】模型压缩是一种缩小已经训练好的神经网络的技术。仅仅使用一小部分计算资源，压缩过的模型的性能，就能和原始模型类似。然而，许多应用程序的瓶颈其实是训练原始的、压缩之前的大型神经网络，没有鸡哪有蛋呀。例如，我们可以在消费级GPU (12gb内存)上训练BERT-base，但需要在谷歌TPU (64gb内存)上训练BERT-large，这阻止了许多尝试训练预训练语言模型的人【1】。

模型压缩领域的结果告诉我们，我们得到的最终压缩结果通常比我们最初训练的大型模型的参数少得多。

但是为什么一定要模型压缩呢？为什么不能从头训练一个高性能的小模型呢？

在这篇文章中，我们将探索从零开始训练小模型所涉及的障碍。我们将讨论为什么模型压缩有效，以及两种提高内存效率的训练方法:超参数化界限和一种能够减少或消除对事后模型压缩的需求的优化算法。

博客原文：

http://mitchgordon.me/machine/learning/2020/01/13/do-we-really-need-model-compression.html

翻译：专知

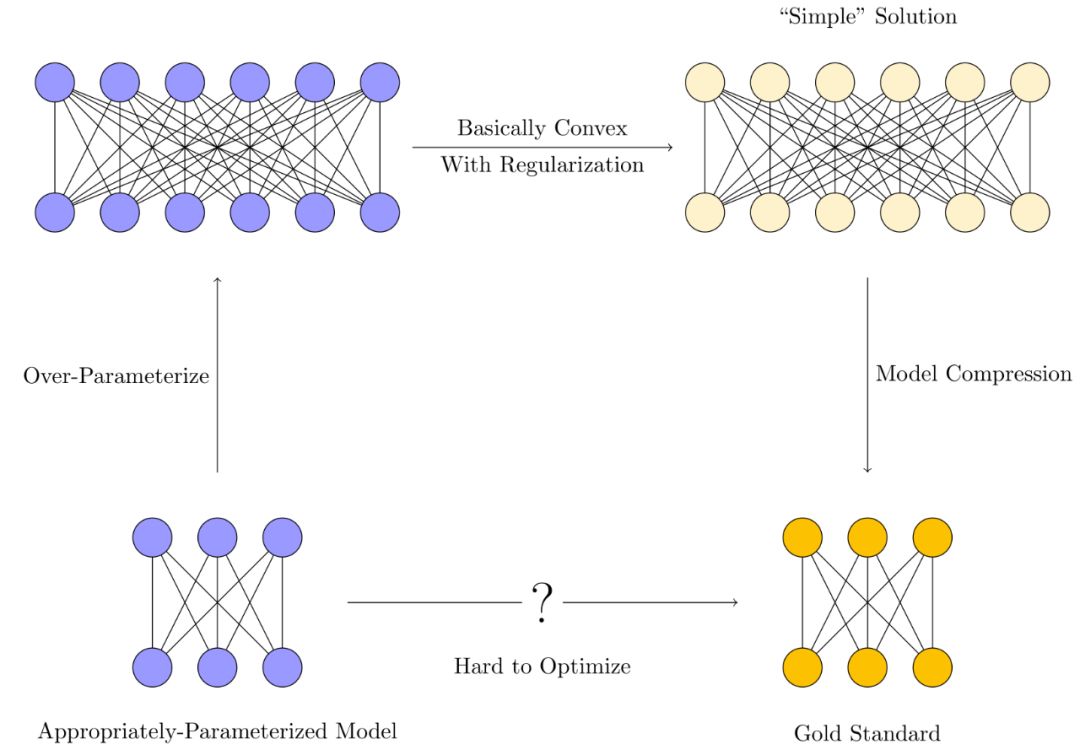
Appropriately-Parameterized Models（适当参数化的模型）

适当参数化的模型(名词)——是指既不过度参数化也不欠参数化的模型，是具有恰好合适数量的参数来表示任务的理想解决方案。

我们通常不会在深度学习范式中训练适当参数化模型。这是因为对于给定的数据集，适当的参数数量通常是未知的。即使已知解，使用梯度下降来训练适当参数化的模型也是出了名的困难【2】。

相反，模型的训练过程通常是这样的:

• 首先，一个过度参数化（Over-parameterize）的模型首先被训练了出来。这些模型的参数通常比训练所用的样本的数量多得多。

• 然后，我们利用各种正则化技术【3】，来约束优化方法，使其更倾向于“简单解决方案（Simple Solution）”，而不是过拟合的。

• 最终，模型压缩技术，希望通过消除冗余，从较大模型中的提取“简单”模型，使内存和时间效率更接近于理想中的适当参数化模型。

极端过参数化的方案，使得训练更加容易。因为模型是过参数化的，它们可以记住完全记住训练数据【4】，而不是学习数据中有用的模式。为此，我们就需要正则化约束它。最后，模型压缩尝试使用各种技术，只保留解决方案实际需要的参数。

由于我们的目标是用更少的GPU 显存来训练神经网络，因此我们实际上想知道一些更直接的问题:

• 非要过度参数化才能训练么?到底需要超采多少参数呢?

• 我们可以通过使用更智能的优化方法来减少过度参数化吗?

  
  

接下来的两节我们将依次讨论这些问题。

Over-parameterization Bounds（过度参数化的界限）

为什么需要过度参数化? 因为，通过对神经网络的过度参数化，我们可以使优化目标，有效的凸化，从而更好的优化。Du【5】和Haeffele【6】已经对一些简单情况进行了数学证明，给出了在多项式时间内实现0训练损失所需的过度参数化的量。

综上：过度参数化是用计算的难易性换取更多的内存使用，即通过提升内存使用的方法，降低问题优化难度。

这些过度参数化的界限通常被认为是松散的。这意味着，虽然我们可以预测足够多的参数来完美地拟合某些数据，但我们仍然不知道完美地拟合数据所需的最小参数数量。从优化过程(SGD vs. GD, Adam vs.其他)到体系结构，严格的界限可能取决于一切变量。计算一个紧界甚至可能比训练所有可能的候选网络在计算上更加棘手。

但这方面肯定还有改进的空间【7】。更严格的过度参数化界限可以让我们训练更小的网络，而不用在架构上进行网格搜索，也不用担心是不是一个更大的网络会给我们带来更好的性能。将证明扩展到递归模型、transformers、批处理，batch norm等模型也存在问题。

Better Optimization Techniques （更好的优化技术）

从经验上讲，适当参数化的模型很难训练。用梯度下降法训练一个适当大小的模型通常会失败得很惨。因为该模型不能很好地拟合训练数据，更不能很好地泛化。这部分是由于神经网络优化过程的不凸性/不友好性，但是训练适当参数化模型的计算复杂度的精确描述仍然是不完整的【8】。

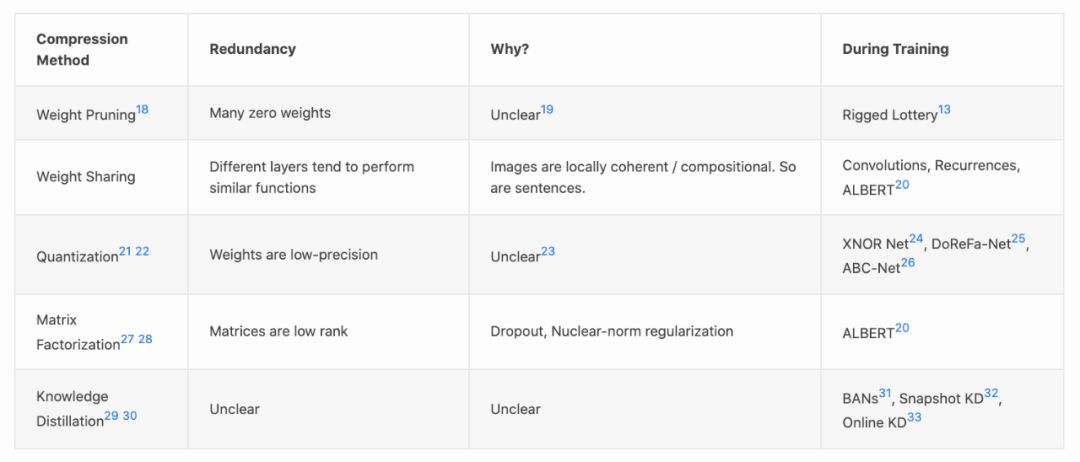
模型压缩技术通过探索过度参数化模型趋向于收敛的解的类型，为我们提供了如何一个如何训练适当参数化模型的线索。模型压缩有很多种，每一种都利用了一种不同类型的“简单性”，这种“简单性”往往出现在训练有素的神经网络中:

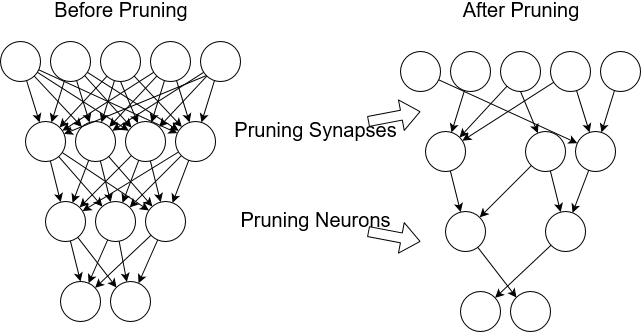
• 许多权重接近于零(剪枝，Pruning)

• 权矩阵是低秩的(权重分解，Weight Factorization)

• 权重可以用少量的比特来表示(比特化，Quantization)

• 层通常学习类似的功能(权重共享，Weight Sharing)

这些“简单性”中的每一个都是由训练过程中的正则化(隐式或其他方式)或训练数据的质量引起的。当我们知道我们正在寻找具有这些性质的解决方案时，我们找到了改进我们的优化技术的新方向。

Sparse Networks from Scratch （从零开始的稀疏网络）

权值剪枝可能是将压缩方法转化为优化改进的最成功示例。经过训练的神经网络通常有许多接近于0的权值(30 - 95%)。在不影响神经网络输出的情况下，可以去掉这些权值。

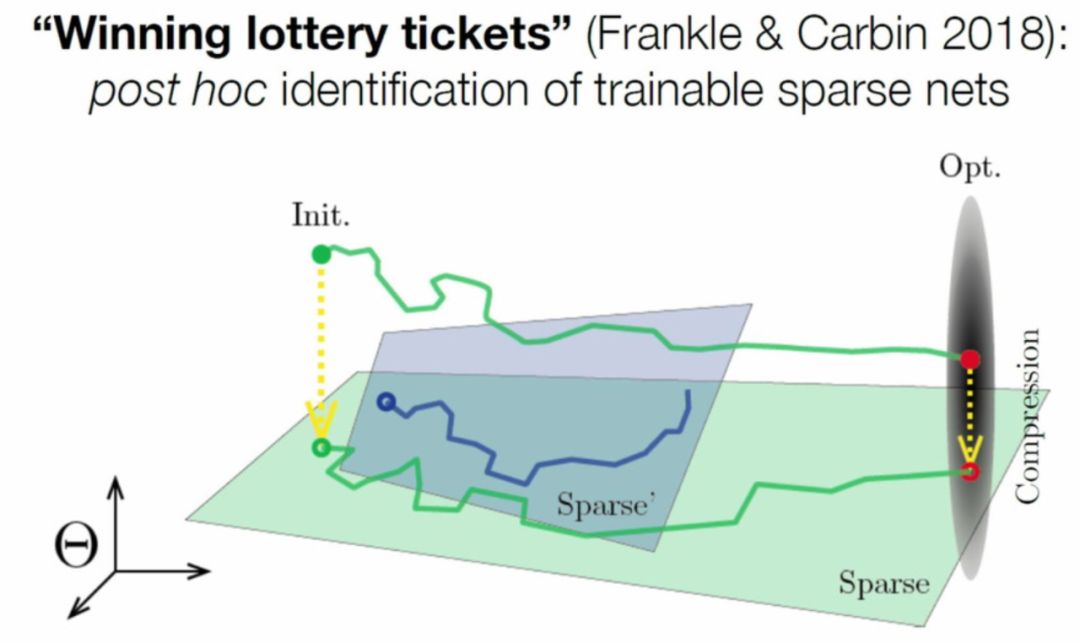
我们是否可以一上来就训练一个稀疏神经网络，而不是事后剪枝?有一段时间，我们认为答案是否定的。稀疏网络很难训练;优化平面是非凸和不友好的。

然而，Frankel和Carbin【9】朝这个方向迈出了第一步。他们发现他们可以从零开始对修剪后的网络进行重新训练，但只有在重新初始化为上次稠密训练中使用的相同初始化时才可以。他们对此的解释是彩票假设:稠密网络实际上是许多并行的适当参数化稀疏模型的随机初始化组合【10】。

最近，Dettmers和Zettlemoyer 【11】、Mostafa et al. 【12】和Evci et al. 【13】已经表明，适当参数化的稀疏网络可以从头开始训练，这大大减少了训练神经网络所需的GPU内存。重要的不是初始化，而是探索模型的稀疏子空间的能力。Lee等人【14】的类似工作尝试通过对数据进行单次遍历来快速找到合适的稀疏架构。

我相信以下一些领域的工作，以后将会频繁出现：

• 揭示了训练神经网络中常见的冗余的模型压缩方法。

• 研究产生这种冗余的归纳偏差/正则化【15】

• 一个更聪明的优化算法被创建出来，用来训练一个从一开始就没有这种冗余的网络。

下面是一个表格，列出了其他类型的模型压缩方法，以及如何让它们更接近训练的开始【16】(不同程度的成功【17】)：

Future Directions （未来的发展方向）

我们真的需要模型压缩吗?这篇文章的标题很有挑衅性，但它的思想并不是:通过收紧过参数化界限和改进我们的优化方法，我们可以减少或消除对事后模型压缩的需要。显然，在我们得到一个明确的答案之前，还有许多悬而未决的问题需要回答。以下是我希望在未来几年内完成的一些工作。

Over-parameterization

• 通过改变数据的质量(使用低资源计算)，我们能得到更严格的界限吗?

• 如果我们使用一个聪明的优化技巧(比如 Rigged Lottery 【13】)，过参数化边界如何变化?

• 我们能得到强化学习环境的过参数化界限吗?

• 我们可以将这些边界扩展到其他常用的架构设计(RNNs、transformer)吗?

Optimization

• 在经过训练的神经网络中，还有其他的冗余我们没有利用吗?

• 使这些实际:

• 从零开始训练比特化的神经网络。

• 从零开始用低秩矩阵训练神经网络。

• 找出为什么知识蒸馏可以改进优化。使用类似的想法来优化，同时使用较少的GPU内存，如果可能的话。

Regularization

• 什么样的正则化会导致什么样的模型冗余?(有一个分类法就好了)

• 修剪和再训练与L0正则化有什么关系?什么隐式正则化导致了剪枝?

• 什么样的正则化可以引入量化?

参考文献：

1. Much more on Deep Learning’s Size Problem. ↩

2. A common example of this is XOR which can theoretically be represented with two hidden neurons but in practice requires using around twenty. ↩

3. Kukačka, Jan, Vladimir Golkov, and Daniel Cremers. 2017. “Regularization for Deep Learning: A Taxonomy.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1710.10686. ↩ ↩2 ↩3

4. Zhang, Chiyuan, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. 2016. “Understanding Deep Learning Requires Rethinking Generalization.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1611.03530. ↩

5. Du, Simon S., Jason D. Lee, Haochuan Li, Liwei Wang, and Xiyu Zhai. 2018. “Gradient Descent Finds Global Minima of Deep Neural Networks.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1811.03804. ↩

6. Haeffele, Benjamin D., and René Vidal. 2017. “Global Optimality in Neural Network Training.” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 7331–39. ↩

7. And it’s very active. I’ve seen a bunch of papers (that I haven’t read) improving on these types of bounds. ↩

8. Theoretically, though, we at least know that training a 3 neuron neural network is NP-hard. There are similar negative results for other specific tasks and architectures. There might be proof that over-parameterization is necessary and sufficient for successful training. You might be interested in this similar, foundational work. ↩

9. Frankle, Jonathan, Gintare Karolina Dziugaite, Daniel M. Roy, and Michael Carbin. 2019. “Linear Mode Connectivity and the Lottery Ticket Hypothesis.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1912.05671. ↩

10. Zhou (2019) explores this idea with more detailed experiments. Liu et al. (2018) found similar results for structured pruning (convolution channels, etc.) instead of weight pruning. They, however, could randomly initialize the structure pruned networks and train them just as well as the un-pruned networks. The difference between these results remains un-explained. ↩

11. Dettmers, Tim, and Luke Zettlemoyer. 2019. “Sparse Networks from Scratch: Faster Training without Losing Performance.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1907.04840. ↩

12. Mostafa, Hesham, and Xin Wang. 2019. “Parameter Efficient Training of Deep Convolutional Neural Networks by Dynamic Sparse Reparameterization.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1902.05967. ↩

13. Evci, Utku, Trevor Gale, Jacob Menick, Pablo Samuel Castro, and Erich Elsen. 2019. “Rigging the Lottery: Making All Tickets Winners.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1911.11134. ↩ ↩2 ↩3

14. Lee, Namhoon, Thalaiyasingam Ajanthan, and Philip H. S. Torr. 2018. “SNIP: Single-Shot Network Pruning Based on Connection Sensitivity.” arXiv [cs.CV]. arXiv. http://arxiv.org/abs/1810.02340. ↩

15. More work is being done on deciding whether lottery tickets are general. ↩

16. Note that model compression is not the only path to memory-efficient training. For example, gradient checkpointing lets you trade computation time for memory when computing gradients during backprop. ↩

17. I would say pruning and weight sharing are almost fully explored at this point, while quantization, factorization, and knowledge distillation have the biggest opportunity for improvements. ↩

18. Gale, Trevor, Erich Elsen, and Sara Hooker. 2019. “The State of Sparsity in Deep Neural Networks.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1902.09574. ↩

19. What type of regularization induces these 0 weights? It’s not entirely clear. Haeffele and Vidal (2017)6 proved that when a certain class of neural networks achieve a global optimum, the parameters of some sub-network become 0. If training impicitly or explicitly prefers L0 regularized solutions, then the weights will also be sparse. ↩

20. Lan, Zhenzhong, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. 2019. “ALBERT: A Lite BERT for Self-Supervised Learning of Language Representations.” arXiv [cs.CL]. arXiv. http://arxiv.org/abs/1909.11942. ↩ ↩2

21. Here’s a survey. Other examples include QBERT and Bitwise Neural Networks. ↩

22. Note that quantized networks need special hardware to really see gains, which might explain why quantization is less popular than some of the other methods. ↩

23. inFERENCe has some thoughts about this from the Bayesian perspective. In short, flat minima (which may or may not lead to generalization) should have parameters with a low minimum-description length. Another explanation is that networks that are robust to noise generalize better, and round-off error can be thought of as a type of regularization. ↩

24. Rastegari, Mohammad, Vicente Ordonez, Joseph Redmon, and Ali Farhadi. 2016. “XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks.” arXiv [cs.CV]. arXiv. http://arxiv.org/abs/1603.05279. ↩

25. Zhou, Shuchang, Zekun Ni, Xinyu Zhou, He Wen, Yuxin Wu, and Yuheng Zou. 2016. “DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients.” https://www.semanticscholar.org/paper/8b053389eb8c18c61b84d7e59a95cb7e13f205b7. ↩

26. Lin, Xiaofan, Cong Zhao, and Wei Pan. 2017. “Towards Accurate Binary Convolutional Neural Network.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1711.11294. ↩

27. Wang, Ziheng, Jeremy Wohlwend, and Tao Lei. 2019. “Structured Pruning of Large Language Models.” arXiv [cs.CL]. arXiv. http://arxiv.org/abs/1910.04732. ↩

28. Denton, Emily, Wojciech Zaremba, Joan Bruna, Yann LeCun, and Rob Fergus. 2014. “Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation.” arXiv [cs.CV]. arXiv. http://arxiv.org/abs/1404.0736. ↩

29. Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. 2015. “Distilling the Knowledge in a Neural Network.” arXiv [stat.ML]. arXiv. http://arxiv.org/abs/1503.02531. ↩

30. Kim, Yoon, and Alexander M. Rush. 2016. “Sequence-Level Knowledge Distillation.” arXiv [cs.CL]. arXiv. http://arxiv.org/abs/1606.07947. ↩

31. Furlanello, Tommaso, Zachary C. Lipton, Michael Tschannen, Laurent Itti, and Anima Anandkumar. 2018. “Born Again Neural Networks.” arXiv [stat.ML]. arXiv. http://arxiv.org/abs/1805.04770. ↩

32. Yang, Chenglin, Lingxi Xie, Chi Su, and Alan L. Yuille. 2018. “Snapshot Distillation: Teacher-Student Optimization in One Generation.” https://www.semanticscholar.org/paper/a167d8a4ee261540c2b709dde2d94572c6ea3fc8. ↩

33. Chen, Defang, Jian-Ping Mei, Can Wang, Yan Feng, and Chun Chen. 2019. “Online Knowledge Distillation with Diverse Peers.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1912.00350. ↩

便捷查看下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“MCDL” 就可以获取《模型压缩》专知资源链接索引

  
  

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

点击“阅读原文”，了解使用专知，查看5000+AI主题知识资料