【NeurIPS 2019】vGraph：联合节点检测与节点表示生成模型- 专知

【NeurIPS 2019】vGraph：联合节点检测与节点表示生成模型

【导读】本文研究了图分析的两个基本任务：集合检测和节点表示学习，它们分别可以获得图的全局和局部结构。在目前的文献中，这两个任务通常是独立研究的，而实际上是高度相关的。我们提出了一个概率生成模型vGraph来协同学习集合和节点表示。具体地说，我们假设每个节点可以表示为一个集合的混合体，并且每个集合被定义为节点上的多项式分布。混合系数和社集合分布通过节点和集合的低维表示来参数化。设计了一种有效的变分推理算法，使邻域节点在潜在空间中的隶属度趋于一致。

论文地址：

https://www.zhuanzhi.ai/paper/81037a8fd360861c33d79d072a4094f3

介绍

图或者网络是一种通用并且灵活的数据结构，可以用于编码对象之间的复杂关系，存在的图结构例如社交网络、航空公司网络、交通网络等。最近图数据在学术界掀起了狂潮，例如社交网络中的节点分类和节点之间关系预测。图网络的分析是一项基本任务，目的是为了将节点聚类为不同的组，每个集合由一组节点组成，不同集合可以获得图结构的全局结构信息。

图分析中的另一个重要的任务是节点表示，这个主要用低维特征描述节点。节点表示有限的获取了局部图结构，并且经常被用来预测任务的特征。

在研究过程中通常会通过聚类获取图的全局结构和嵌入的方式获得局部节点表示。聚类的方法通常用于探索性分析，而节点嵌入通常用于预测性分析。但是这两个任务关联紧密，通常会同时执行。

在本文中，我们提出了一种称为vGraph的新型概率模型，用于联合节点监测和节点表示学习。vGraph假设每个节点可以表示为多个集合的混合，并通过在集合z上的多项式分布来描述，即p(z|v)，同时，将每个集合z建模为节点v的分布：p(v|z)。vGraph对每个节点生成邻居的过程建模，给定一个节点u，我们先从p(z|u)对u进行分配。给定集合分配z，通过集合分布p(v|z)获取与节点v的之间的边（u.v）。我们还设计了一个有效的反向传播算法，用变分推理来最大化似然估计。由于数据是离散的，我们采用Gumbel-Softmax，受有频谱聚类方法的启发，在变分推理的过程中添加了平滑正则项，以确保相邻节点的相似性。

在实验部分，我们显示了三个任务的结果：重叠集合检测、不重叠集合检测和节点分类。所有的这些都使用公开数据集来实现。

相关工作

集合检测

许多集合检测都依赖于矩阵分解，通常，这些方法都通过对图邻接矩阵或其他相关矩阵进行低秩分解来恢复节点集合关系矩阵，由于矩阵分解的复杂性而无法扩展，并且它的性能受到双线性模型容量的限制。还有其他各种方法被提出用于解决集合检测问题，与这些方法相比，vGraph具有更高的可扩展性，并且vGraph还可以通过反向传播和Gumbel-Softmax进行优化，此外，vGraph还能够学习并利用节点表示进行集合检测。

节点表示

节点表示的目的是学习图中节点的分布式表示，这样可以使相似节点趋向于相似的表示。通常的方法都使用广度优先搜索或深度优先搜索来探索每个节点的连接性。尽管这些方法在各种应用程序上都十分有效，但是这些方法都集中在保留图的局部结构上，因此会忽略全局信息。在 vGraph，标签可以提供上下文信息，使节点表示能够获取全局信息。

混合模型

从方法上看，我们的方法与混合模型相关，尤其是主题模型。vGraph使用节点和集合嵌入对分布进行参数化，并对所有参数进行反向传播训练。

方法

本部分，我们将详细介绍 vGraph，我们的方法假设每个节点都属于不同环境中的多个集合，并且不同环境中的节点要生成不同的邻居。vGraph通过节点和集合嵌入来参数化节点-集合分布，这样可以从集合的检测中受益于节点表示，同样，检测到的集合分配又可以改善节点表示，我们增加的平滑规则化术语，该术语链接的节点位于相同的集合中。

vGraph

假设每个节点可以属于多个集合，对于每个节点，将根据集合的上下文生成不同的邻居，我们为每个节点w引入先验分布p(z|w)，为每个集合引入节点分布p(c|z)，每个边(w，c)的生成过程可以表征如下：对于节点w，我们首先绘制一个集合分配 z ∼ p(z|w)，表示生成过程中的w的环境，然后根据分配z到c ∼ p(c|z)生成链接的邻居c，此生成过程可以用概率表述：

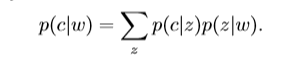
vGraph通过引入一组节点嵌入和集合嵌入来对分布p（z | w）和p（c | z）进行参数化，节点嵌入的不同集合用于参数化两个分布，具体来说，让 φi表示分布p(z|w)中使用的节点i的嵌入，ϕi表示p(c|z)中节点i的嵌入，而ψj表示第j个集合的嵌入，通过两个softmax对先验分布进行参数化：

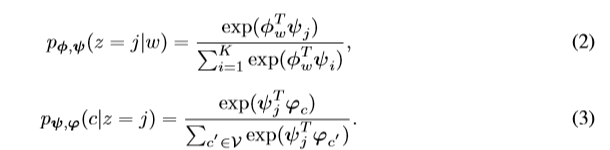
公式3需要对所有顶点求和，因此，对于大型数据集，我们将采用以下目标函数：

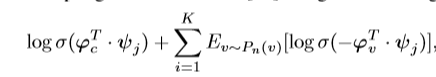
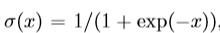
P_n(v)是个噪音分布，K值负样本总数，这样，结合随机优化，可以使模型具有可扩展性。为了学习vGraph的参数，我们尝试最大化边缘对数似然值，由于直接优化此目标难以解决，因此我们优化以下函数：

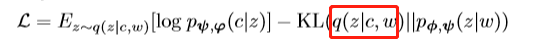
q是一个变分分布，KL代表两个分布之间的KL散度。我们采用神经网络将变分分布q参数化：

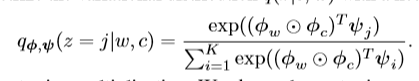
变分分布q表示边(w,c)的集合成员，基于此，我们可以汇总所有邻居，从而估算每个节点w的集合分布：

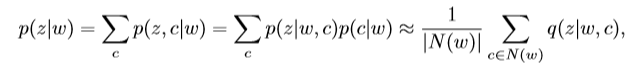
这里，N(w)表示的是w的邻居节点集合，为了推断非重叠集合，我们采用argmax计算，当我们计算重叠集合时，用以下计算方式代替阈值p(z|w)：

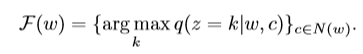
也就是说，我们将每个边分配到一个集合中，然后通过收集入射到每个边缘集合内所有边缘的节点，将边缘集合映射到节点集合。

光滑正则优化

为了优化，我们需要优化下限变分分布中的参数和生成参数，如果z是连续的，则可以使用重参数化技巧，但是我们的数据z是离散的，原则上，我们仍然使用分数计算器来计算梯度，然而，结果仍会具有高方差，因此，我们使用Gumbel-Softmax重新参数化来获得梯度。

集合可以定义为一组节点，这些节点之间的相似度高于该组外部的相似性，如果两个节点连接并且共享相似的邻居，则它们是相似的。但是， vGraph不会以这种方式来获得局部连接。为了解决这个问题，我们采用平滑正则化来完成，正则化项如下所示：

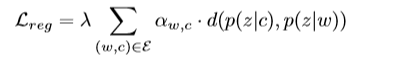
这里λ是一个参数，a是正则权重，d指的是两个分布之间的距离。a的计算公式如下：

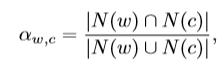
上式表示的是两个节点之间的相似性，值越大表明两个节点在集合中相似分布越多。损失函数如下：

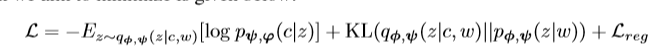
等级 vGraph

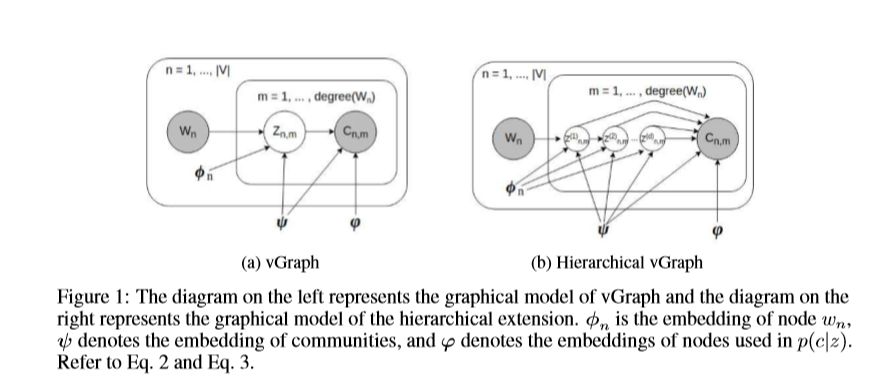
vGraph框架的优势之一是它非常通用，可以自然扩展以检测层次结构社区。在这种情况下，假设有一个d级树，并且每个节点都与一个集合相关联，则集合分配可以表示为d维路径向量，如fig 1,生成过程的公式如下：

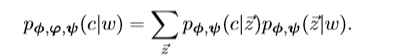
树的每个节点上，都有一个与集合相关联的嵌入向量，这种方法类似于语言模型中使用的分层softmax参数化。

实验

由于vGraph可以检测重叠社区和不重叠社区，因此我们在三个任务上对其进行评估：重叠集合检测，不重叠集合检测和顶点分类。

数据

我们在20个图形数据上评估 vGraph ，对于不重叠的集合检测和节点分类，我们分别使用6个数据集：Citeseer, Cora, Cornell, Texas, Washington, 和Wisconsin。对不重叠集合，我们使用14个数据集：Facebook, Youtube, Amazon, Dblp, Coauthor-CS等。为了演示方法的可扩展性，我们在DBLP-full上进行了可视化。

评估指标

对于重叠集合检测，使用F1-score和jaccard相似度来测量检测到的集合性能；对于不重叠的集合检测，我们使用归一化和模块化方法。对于节点分类，使用 Micro-F1 和 Macro-F1。

对比试验

重叠集合检测，baseline分别为：BigCLAM、CESNA、SVI
不重叠集合检测，baseline分别为：MF、DeepWalk、LINE、Node2vec、ComE。

实验设置

所有baseline都按作者的默认参数，对于仅输出节点表示的方法，我们使用K-means来获得非重叠集合。所示结果为5次运行的平均值。当不同方法的集合数量不同时，很难比较结果的质量，因此，将K设置为所有方法的真实集合数。对于vGraph，当数据集比较少的时候，就使用全批次训练，反之就设置为5000或10000的随机训练。学习率设置为0.005，每100次迭代后递减0.99，使用Adam优化器，并进行5000次迭代训练，使用平滑度正则化时，将λ设置为100。在所有方法的所有实验中，节点嵌入的维数均设置为128。对于节点分类任务，我们随机选择70％的标签进行训练，其余的进行测试。

结果

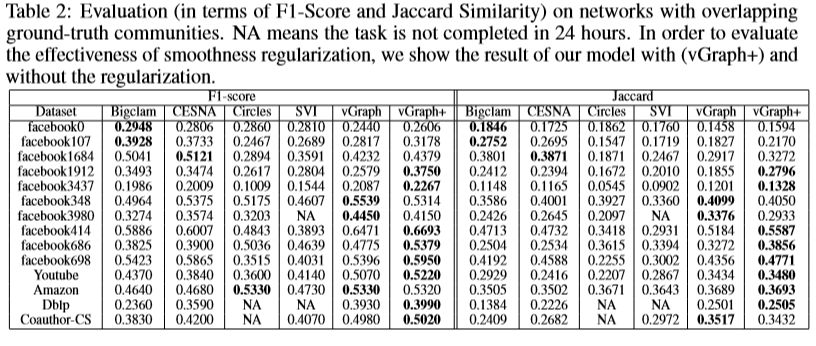
表2显示了重叠集合的结果。vGraph在F1得分或Jaccard相似性方面优于14个数据集中的11个数据集中的所有基线方法，因为它能够在节点级别上利用有用的表示形式。此外，vGraph在这些数据集上也非常有效，因为我们使用了变分分布并通过节点和社区嵌入对模型进行了参数化。通过添加平滑度正则化项（vGraph +），我们看到了更高的性能，这表明我们的方法可以与传统检测方法中的概念相结合。

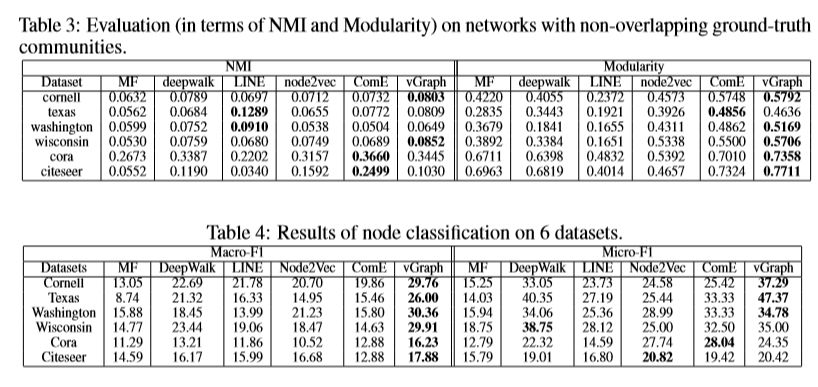
表3列出了非重叠集合检测的结果。就NMI而言，vGraph优于6个数据集中的4个数据集中的所有常规节点嵌入+ K均值，而模块化方面则优于所有6个数据集。ComE是共同解决节点嵌入和社区检测的另一个框架，通常也比其他节点嵌入方法+ K-Means更好。这表明通过协作而不是按顺序学习这两个任务可以进一步提高性能。与ComE相比，就NMI而言，vGraph在6个数据集中的4个数据集中表现更好，而在模块化方面，则6个数据集中的5个数据表现更好。

表4显示了节点分类任务的结果。在12个数据集中的9个数据集中，vGraph的性能明显优于所有baseline。原因是大多数baseline仅考虑局部图信息，而没有对全局语义建模。vGraph通过将节点嵌入表示为社区的混合物来合并全局上下文来解决此问题。

可视化

上图（a）为facebook107数据集的可视化。为了证明模型可以应用于大型网络，在图（b）中具有100000个节点和330000个边的网络上展示了可视化结果。为了演示模型的层次扩展，在图3中可视化了数据集的子集，分别在（a）和（b）可视化了第一层和第二层集合。

结论

在本文，提出vGraph，这是一种执行重叠（和不重叠）集合检测并同时学习节点和集合嵌入的方法。vGraph将图形中边的生成转换为推理问题。为了集合检测和节点表示学习之间的协作，我们假设每个集合定义为节点上的多项式分布。还在潜在空间中设计了一个平滑度正则化器，以获取相似的相邻节点。对20个不同基准数据集的经验评估表明，该方法在两项任务上的有效性。