贝叶斯卷积神经网络：架起深度学习与统计学的桥梁-附PDF下载- 专知

贝叶斯卷积神经网络：架起深度学习与统计学的桥梁-附PDF下载

【导读】概率编程允许我们建立小而专注的模型深入了解数据；另一方面，深度学习可以运用许多启发式的方法来训来拿大而复杂的模型，获得较好的预测效果。最近在变分推理上的创新允许概率编程处理复杂模型和大数据量。结合这两种方法可以获得一些新的创新。本文作者就是重点研究贝叶斯模型与传统的卷积神经网络的融合，这是他的硕士论文，作者也提供了论文的源码供大家学习掌握。

【摘要】

人工神经网络是一种连接主义的系统，它通过学习实例来完成给定的任务，而不需要事先了解该任务。这是通过在每个节点中找到权重的最佳点估计来完成的。一般情况下，使用点估计作为权重的网络在大数据集上表现良好，但是它们无法在数据很少或没有数据的区域中表达不确定性，从而导致过度拟合的情况。

本文提出了基于变分推理的贝叶斯卷积神经网络(BayesCNN)，该网络引入了权值上的概率分布。此外，本文提出的BayesCNN架构还可应用于图像分类，图像超分辨率和生成对抗网络等任务。

BayesCNN是建立在贝叶斯的基础上的，它通过Backprop得到真实后验的变分近似。我们提出的方法不仅在相同的体系结构中实现了与频率推理相当的性能，而且还包含对不确定性和正则化的测量。进一步消除了模型中drop的使用。此外，我们推断出模型预测是如何基于认知和任意不确定性的，最后，我们提出了修剪贝叶斯结构并使其更具计算性和时间效率的方法。

在论文的第一部分，解释了贝叶斯神经网络，并将其应用于图像分类任务。将结果与基于点估计的架构MNIST，CIFAR-10和CIFAR-100数据集进行比较。此外，计算了系统的不确定性，对系统的结构进行了修剪，并对结果进行了比较。

在论文的第二部分，将这一概念进一步应用于其他计算机视觉任务，即图像超分辨率和生成对抗网络。对BayesCNN的概念进行了测试，并与类似领域中的其他概念进行了比较。

【论文和代码地址】

https://github.com/kumar-shridhar/Master-Thesis-BayesianCNN

https://github.com/kumar-shridhar/PyTorch-BayesianCNN

【论文下载】

请关注专知公众号（点击上方蓝色专知关注）

后台回复“贝叶斯卷积神经网络” 就可以获取本文的下载链接~

专知《深度学习：算法到实战》2019年今晚8点开讲PyTorch基础，欢迎扫码报名！

【Intro简介】

深度神经网络（DNN）是连接系统，它通过学习示例来学习执行任务，而无需事先了解任务。它们可以轻松扩展到数百万个数据点，并且可以通过随机梯度下降进行优化。

卷积神经网络（CNN），是DNN的变体，在图像分类领域已经超过了人类的准确性(e.g.[24,56,34])。由于CNN能够适应各种非线性数据点，因此需要大量的训练数据。这通常使CNN和神经网络在小数据集上易于过度拟合。该模型较好地拟合了训练数据，但不能预测新数据。这通常使神经网络无法正确评估训练数据中的不确定性，从而导致对正确的类别，预测或行为作出过度自信的决定，即过拟合。

在实际应用中，控制过拟合的各种正则化技术有，early stopping,重量衰减（weight decay），L1，L2正则化，并且目前最流行和有效的技术是dropout。

1.1 问题描述

尽管神经网络架构在几乎所有分类任务中都取得了最先进的结果，但神经网络仍然会做出过度自信的决策。目前的神经网络结构中缺少对预测不确定性的度量。需要非常仔细的训练，需要采取权重控制措施，如权重的正则化和类似技术，以使模型不易受过度拟合问题的影响。

本文通过在卷积神经网络中引入贝叶斯学习来解决这两个问题。贝叶斯学习在卷积神经网络的预测中增加了不确定性和正则化。

1.2 现状

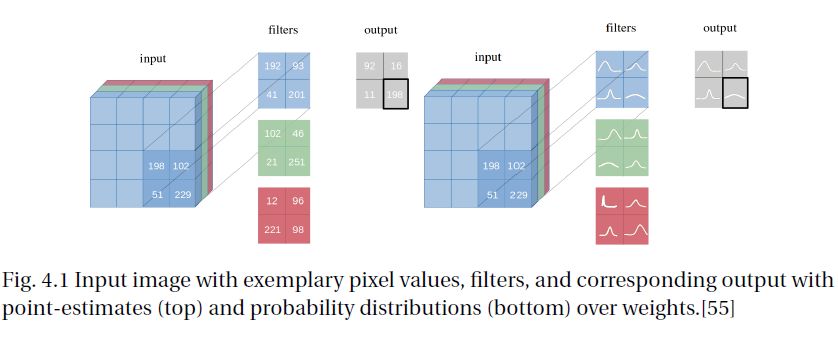
深度神经网络已成功应用于许多领域，包括非常敏感的领域，如医疗保健，安全性，欺诈性交易等等。然而，从概率论的角度来看，使用单点估计作为权重来建立任何分类都是不合理的。另一方面，贝叶斯神经网络对过拟合具有较强的鲁棒性，可以很容易地从小数据集中学习。贝叶斯方法通过其参数以概率分布的形式进一步提供不确定性估计（见图1.1）。同时，利用先验概率分布对参数进行积分，在训练过程中计算多个模型的平均值，使网络具有正则化效果，从而防止过拟合。

神经网络参数的贝叶斯后验推断是控制过拟合的一种具有理论吸引力的方法；然而，对CNN的内核（也称为滤波器）上的分布进行建模以前从未成功过，这可能是因为在实际应用中通常使用大量参数和非常大的模型。

在贝叶斯神经网络中，即使只有少量的参数，后验模型的推断也是一项困难的任务。通常使用模型后验的近似值，变分推理是一种流行的方法。在这种方法中，可以使用简单的变分分布（例如高斯分布）对后验进行建模，并尝试使分布的参数尽可能接近真实的后验。这是通过最小化Kullback-Leibler与真实后验的分歧来完成的。许多人过去都采用过这种方法来制定标准的NN模型。但是用于逼近贝叶斯神经网络后验的变分方法在计算上可能相当昂贵 - 使用高斯近似分布会大大增加模型参数的数量，而不会大幅增加模型容量。以Blundell等人为例，使用高斯分布进行贝叶斯后验近似，使模型参数的数量增加了一倍，但与传统的使用drop方法的预测性能相同。这使得该方法在实践中不适合与CNNs一起使用，因为参数数量的增加代价太大。

论文工作的主要贡献如下：