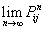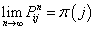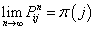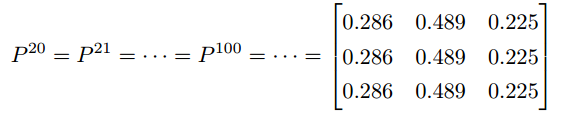1、马氏链及其平稳分布
马氏链的数学定义很简单
P(Xt+1=x∣Xt,Xt−1,⋯)=P(Xt+1=x∣Xt)
也就是状态转移的概率只依赖于前一个状态。
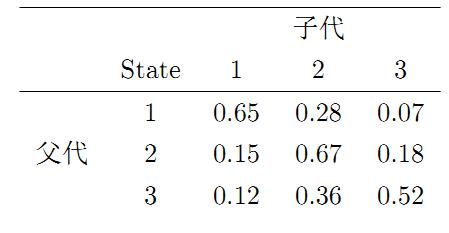
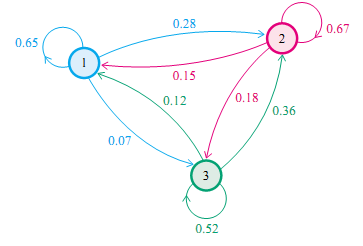
我们先来看马氏链的一个具体的例子。社会学家经常把人按其经济状况分成3类:下层(lower-class)、中层(middle-class)、上层(upper-class),我们用1,2,3分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别,那么他的孩子属于下层收入的概率是0.65, 属于中层收入的概率是 0.28, 属于上层收入的概率是0.07。事实上,从父代到子代,收入阶层的变化的转移概率如下:
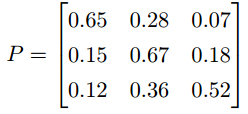
使用矩阵的表示方式,转移概率矩阵记为
假设当前这一代人处在下层、中层、上层的人的比例是概率分布向量
π0=[π0(1),π0(2),π0(3)],那么他们的子女的分布比例是
π1=π0P。他们的孙子代的比例将是
π2=π1P=π0P2,….,第n代子孙的收入分布比例将是
πn=πn−1P=π0Pn:
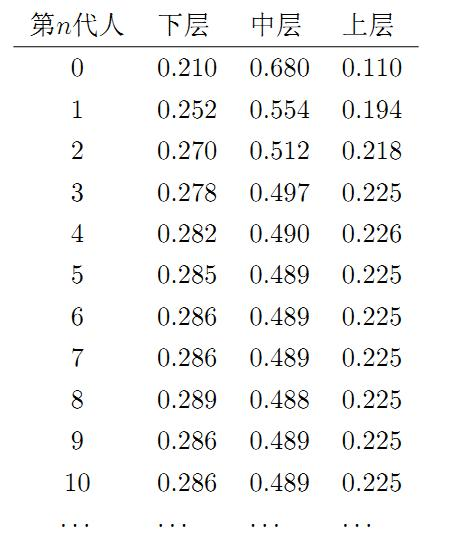
假设初始概率分布为π0=[0.21,0.68,0.11],则我们可以计算前n代人的分布状况如下:
我们发现从第7代人开始,这个分布就稳定不变了,这个是偶然的吗?我们换一个初始概率分布
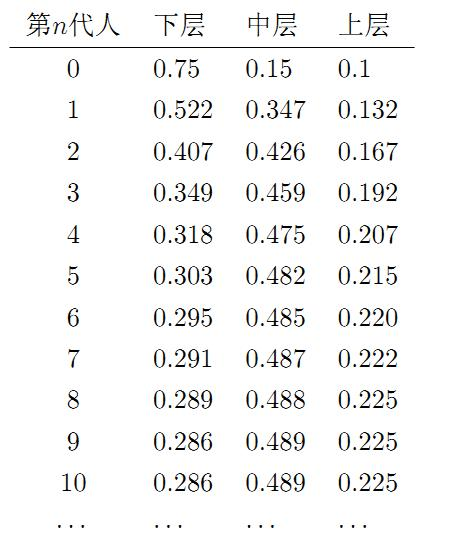
π0=[0.75,0.15,0.1]试试看,继续计算前n代人的分布状况如下:
我们发现,到第9代人的时候,分布又收敛了。最为奇特的是,两次给定不同的初始概率分布,最终都收敛到概率分布
π=[0.286,0.489,0.225],也就是说收敛的行为和初始概率分布
π0无关。这说明这个收敛行为主要是由概率转移矩阵
P决定的。我们计算一下
Pn。
我们发现,当 n足够大的时候,这个矩阵的每一行都是稳定地收敛到
π=[0.286,0.489,0.225]这个概率分布。自然的,这个收敛现象并非是我们这个马氏链独有的,而是绝大多数马氏链的共同行为,关于马氏链的收敛我们有如下漂亮的定理:
马氏链定理:如果一个非周期马氏链具有转移概率矩阵
P,且它的任何两个状态是连通的,那么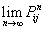 存在且与i无关,记
存在且与i无关,记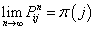 ,我们有:
,我们有:

-
π(j)=i=0∑∞π(j)Pij
-
π是方程
πp=π的唯一非负解,其中:$\pi $称为马氏链的平稳分布。
π=[π(1),π(2),⋯,π(j),⋯],i=0∑∞πi=1
这个马氏链的收敛定理非常重要,所有的 MCMC(Markov Chain Monte Carlo)
方法都是以这个定理作为理论基础的。
定理的证明相对复杂,一般的随机过程课本中也不给证明,所以我们就不用纠结它的证明了,直接用这个定理的结论就好了。我们对这个定理的内容做一些解释说明:
-
该定理中马氏链的状态不要求有限,可以是有无穷多个的;
-
定理中的“非周期“这个概念我们不打算解释了,因为我们遇到的绝大多数马氏链都是非周期的;
-
两个状态i,j是连通并非指i 可以直接一步转移到j(
Pij>0),而是指i可以通过有限的n步转移到达j(
Pij>0)。马氏链的任何两个状态是连通的含义是指存在一个n,使得矩阵
Pn中的任何一个元素的数值都大于零。
我们用
Xi表示在马氏链上跳转第i步后所处的状态,如果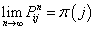 存在,很容易证明以上定理的第二个结论。由于
存在,很容易证明以上定理的第二个结论。由于
P(Xn+1=j)=i=0∑∞P(Xn=i)P(Xn+1=j∣Xn=i)=i=0∑∞P(Xn=i)Pij
上式两边取极限就得到
π(j)=i=0∑∞π(i)Pij
从初始概率分布
π0出发,我们在马氏链上做状态转移,记
Xi的概率分布为
πi则有
X0∼π0(x),Xi∼πi(x)
πi(x)=πi−1(x)P=π0(x)Pn
由马氏链收敛的定理, 概率分布
πi(x)将收敛到平稳分布
π(x)。假设到第n步的时候马氏链收敛,则有
X0∼π0(x)
X1∼π1(x)
Xn∼πn(x)=π(x)
Xn+1∼π(x)
Xn+2∼π(x)
所以
Xn,Xn+1,Xn+2,⋯∼π(x)都是同分布的随机变量,当然他们并不独立。如果我们从一个具体的初始状态
x0开始,沿着马氏链按照概率转移矩阵做跳转,那么我们得到一个转移序列
x0,x1,x2,⋯xn,xn+1⋯,由于马氏链的收敛行为,
xn,xn+1⋯都将是平稳分布
π(x)的样本。