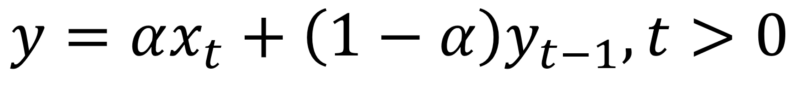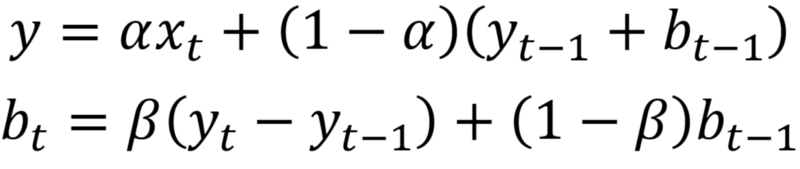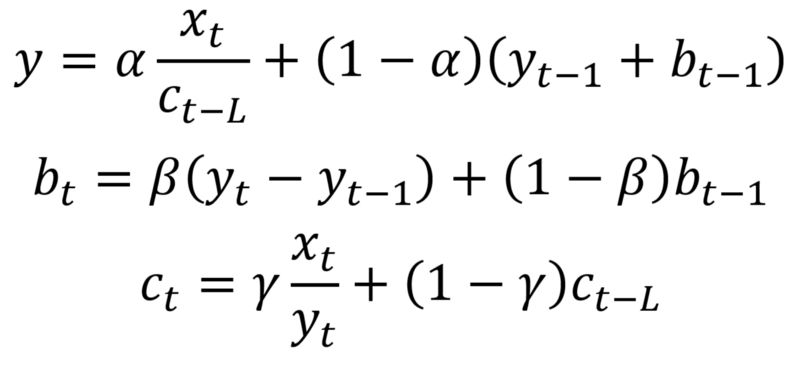关于时间序列你需要了解的一切
【导读】了解时间序列处理的各种方法,包括移动平均线,指数平滑,平稳性,自相关,SARIMA等。
作者 | Marco Peixeiro
编译 | Xiaowen
摄影:Lukas Blazek
无论我们是希望预测金融市场的趋势还是电力消耗,时间都是我们模型中必须考虑的重要因素。例如,不仅知道股票会价格上涨,而且要知道何时会上涨。
输入时间序列。时间序列只是一系列排序的数据点。在时间序列中,时间通常是自变量,目标通常是对未来进行预测。
但是,在处理时间序列时还有其他方面可以发挥作用。
它是静止的吗?
有季节性吗?
目标变量是否自相关?
在这篇文章中,我将介绍时间序列的不同特征以及我们如何对它们进行建模以获得准确(尽可能多)的预测。
自相关性
不严谨地说,自相关是观察对象之间的相似性,是它们之间的时间延迟的函数。
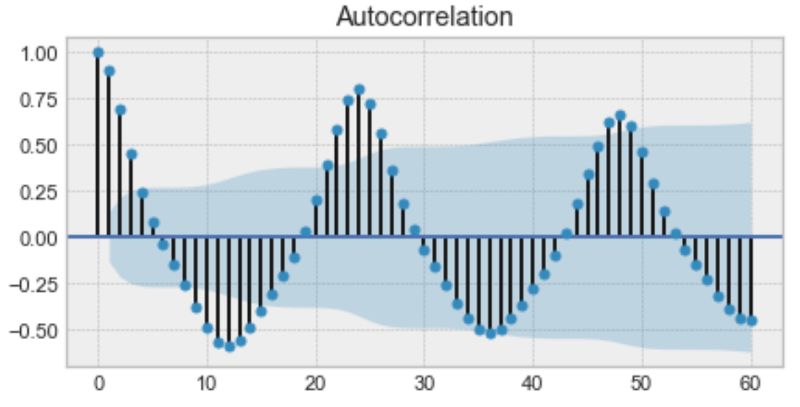
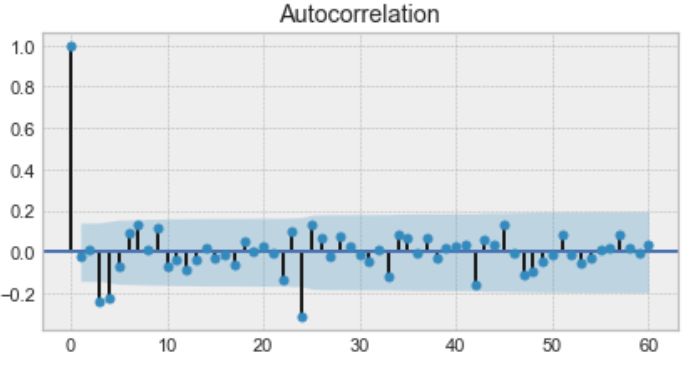
自相关图的示例
以上是自相关图的示例。仔细观察,你会发现第一个值和第24个值具有很高的自相关性。同样,第12和第36次观察是高度相关的。这意味着我们会在每24个单位时间内找到一个非常相似的值。
请注意该图如何看起来像正弦函数。这是季节性的暗示,你可以通过查找上图中的周期来找到它的值——24小时。
季节性
季节性是指周期性波动。例如,白天电力消耗高,夜间电力消耗低,圣诞节期间网上销售增加,然后再次放缓。
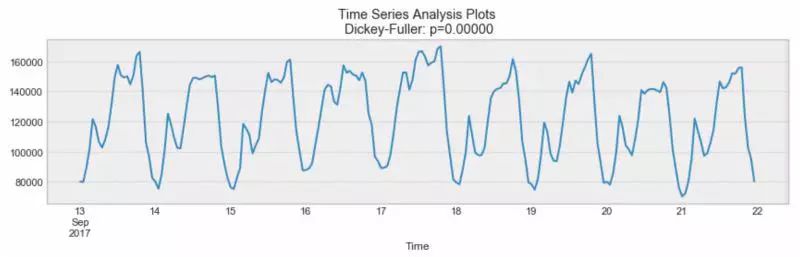
季节性的例子
如你所见,每日季节性都很明显。每天,你都会看到一个晚上的高峰,最低点是每天的开始和结束。
请记住,季节性也可以从自相关图中得出,如果它具有正弦曲线形状的话。
平稳
平稳性是时间序列的重要特征。如果时间序列的统计特性不随时间变化,则称其为静止的。换句话说,它具有恒定的均值和方差,协方差与时间无关。
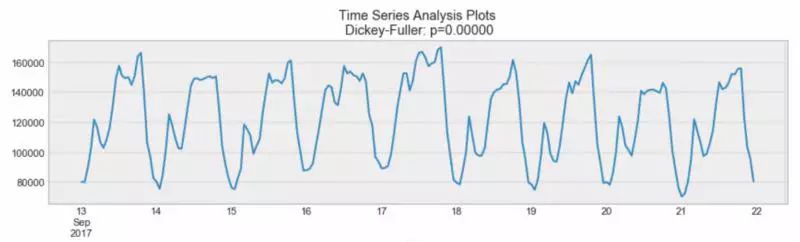
固定过程的示例
再看一下同一个图,我们看到上面的过程是平稳的。均值和方差不随时间变化。
通常,股票价格不是一个固定的过程,因为我们可能会看到一个增长的趋势,或者它的波动性可能会随着时间的推移而增加(意味着方差正在发生变化)。
理想情况下,我们希望有一个固定的时间序列进行建模。当然,并非所有这些都是静止的,但我们可以进行不同的变换以使它们静止。
如何测试过程是否静止
你可能已经注意到Dickey-Fuller上方的情节标题。这是我们运行的统计测试,用于确定时间序列是否静止。
在不进入Dickey-Fuller测试的技术性的情况下,它测试了单位根存在的零假设。
如果是,则p> 0,并且该过程不是静止的。
否则,p = 0,拒绝零假设,并且该过程被认为是静止的。
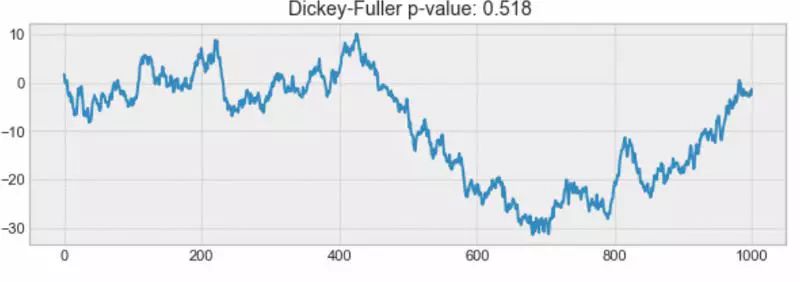
例如,下面的过程不是固定的。注意平均值是如何随时间变化的。
非固定过程的示例
建模时间序列
有许多方法可以对时间序列进行建模以进行预测。在这里,我将介绍:
· 移动平均线
· 指数平滑
· ARIMA
移动平均线
移动平均模型可能是最简单的时间序列建模方法。该模型简单地说明下一次观察是所有过去观察的平均值。
虽然简单,但这个模型可能出奇的好,它代表了一个很好的起点。
否则,移动平均线可用于识别数据中的有趣趋势。我们可以定义一个窗口来应用移动平均模型来平滑时间序列,并突出显示不同的趋势。
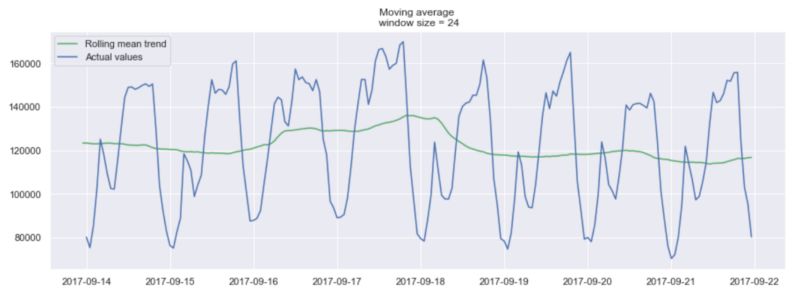
24小时窗口的移动平均值示例
在上图中,我们将移动平均模型应用于24h窗口。绿线平滑了时间序列,我们可以看到24小时内有2个峰值。
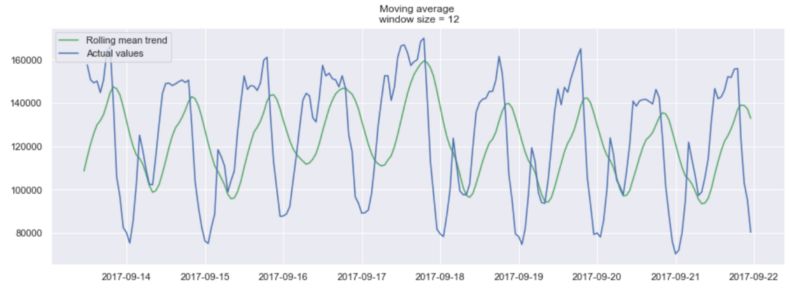
当然,窗口越长,趋势就越平滑。以下是较小窗口的移动平均值示例。
12h窗口的移动平均值示例
指数平滑
指数平滑使用与移动平均值类似的逻辑,但这次,为每个观测值分配不同的减小权重。换句话说,随着我们进一步远离现在时刻,观察对象的重要性降低。
数学上,指数平滑表示为:
指数平滑表达式
在这里,alpha是一个平滑因子,它取0到1之间的值。它决定了之前观察的权重减少的速度。
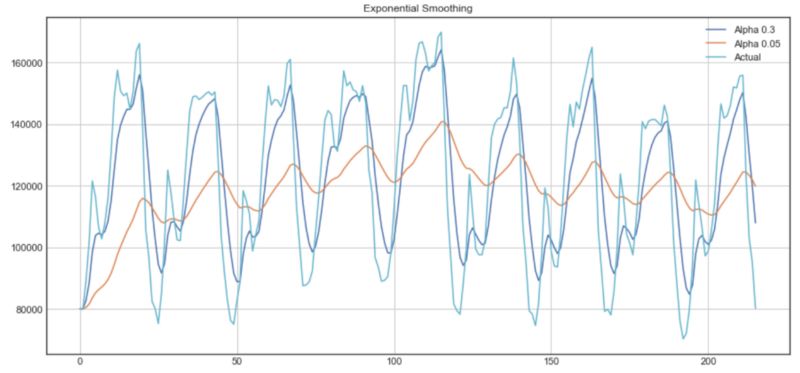
指数平滑的示例
从上图中,深蓝色线表示使用平滑因子0.3的时间序列的指数平滑,而橙色线使用0.05的平滑因子。
如你所见,平滑因子越小,时间序列越平滑。这是有道理的,因为当平滑因子接近0时,我们接近移动平均模型。
双指数平滑
当时间序列中存在趋势时,使用双指数平滑。在这种情况下,我们使用这种技术,这只是指数平滑两次的递归使用。
数学上双指数平滑表达式:
这里,beta是趋势平滑因子,它取0到1之间的值。
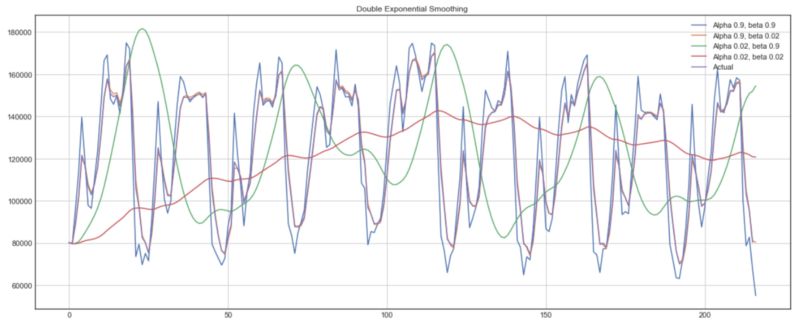
下面,你可以看到alpha和beta的不同值如何影响时间序列的形状。
双指数平滑的示例
Tripe指数平滑
此方法通过添加季节性平滑因子来扩展双指数平滑。当然,如果你注意到时间序列中的季节性,这将非常有用。
数学上,三指数平滑表示为:
三指数平滑表达式
其中gamma是季节性平滑因子,L是季节的长度。
季节性自回归整合移动平均模型(SARIMA)
SARIMA实际上是简单模型的组合,可以制作一个复杂的模型,可以模拟表现出非平稳特性和季节性的时间序列。
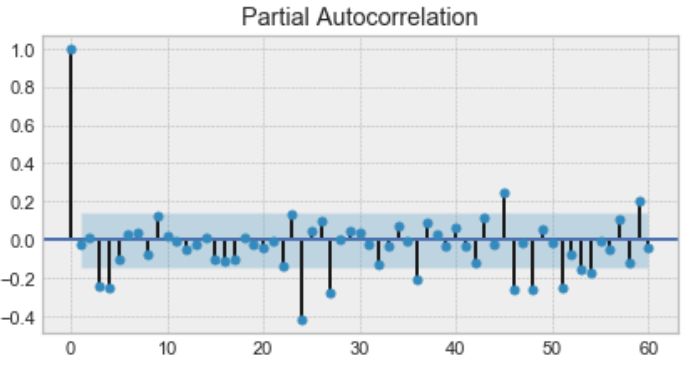
首先,我们有自回归模型AR(p)。这基本上是时间序列回归到自身。在这里,我们假设当前值取决于其先前的值有一些滞后。它需要一个参数p来表示最大滞后。为了找到它,我们查看部分自相关图并确定滞后,在此之后大多数滞后不显着。
在下面的示例中,p=4。
部分自相关图的示例
然后,我们添加移动平均模型MA(q)。这需要一个参数q,它代表最大滞后,此后其他滞后在自相关图上不显着。
下面,q=4。
自相关图的示例
之后,我们添加集成顺序 I(d)。参数d表示使系列静止所需的差异数。
最后,我们添加最终组件:季节性S(P,D,Q,s),其中s只是季节的长度。此外,该组件需要与p和q相同的参数P和Q,但是对于季节性组件。最后,D是季节性整合的顺序,表示从系列中删除季节性所需的差异数量。
结合所有,我们得到SARIMA(p,d,q)(P,D,Q,s)模型。
从中可以看出,在使用SARIMA建模之前,我们必须对我们的时间序列应用变换来消除季节性和任何非平稳行为。
这是时间序列!这是一个独立的领域,机器学习工程师可以专注于时间序列。它还有很多,但这是进一步探索的良好起点。
原文链接:
https://towardsdatascience.com/almost-everything-you-need-to-know-about-time-series-860241bdc578
-END-
专 · 知
专知《深度学习:算法到实战》课程全部完成!470+位同学在学习,现在报名,限时优惠!网易云课堂人工智能畅销榜首位!
请加专知小助手微信(扫一扫如下二维码添加),咨询《深度学习:算法到实战》参团限时优惠报名~

欢迎微信扫一扫加入专知人工智能知识星球群,获取专业知识教程视频资料和与专家交流咨询!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
点击“阅读原文”,了解报名专知《深度学习:算法到实战》课程