手把手教你学习神经网络的数学原理（代码和教程）- 专知

会员服务 ·

手把手教你学习神经网络的数学原理（代码和教程）

专知出品

【导读】推荐一个GitHub的教程—神经网络的数学图解，详细介绍了浅层神经网络的定义、初始化、前向传播、反向传播的细节以及代码实现，和实验结果，手把手介绍其数学原理，希望新手收藏学习。

作者：Omar U. Florez

编译：专知

神经网络是线性和非线性模块的巧妙组合。当我们明智地选择并连接它们时，我们就有了一个强大的工具来近似拟合任何数学函数。例如，用非线性决策边界分类的方法。

反向传播技术负责更新可训练参数，尽管它具有直观和模块化的特性，但这一概念并不总是得到深入的解释。让我们从头开始构建一个神经网络，看看神经网络的内部功能，我们将模块类比为乐高积木块，一次一块积木叠加。

实现此功能的代码可以在这个repository中找到:

https://github.com/omar-florez/scratch_mlp

神经网络作为一个组成部分

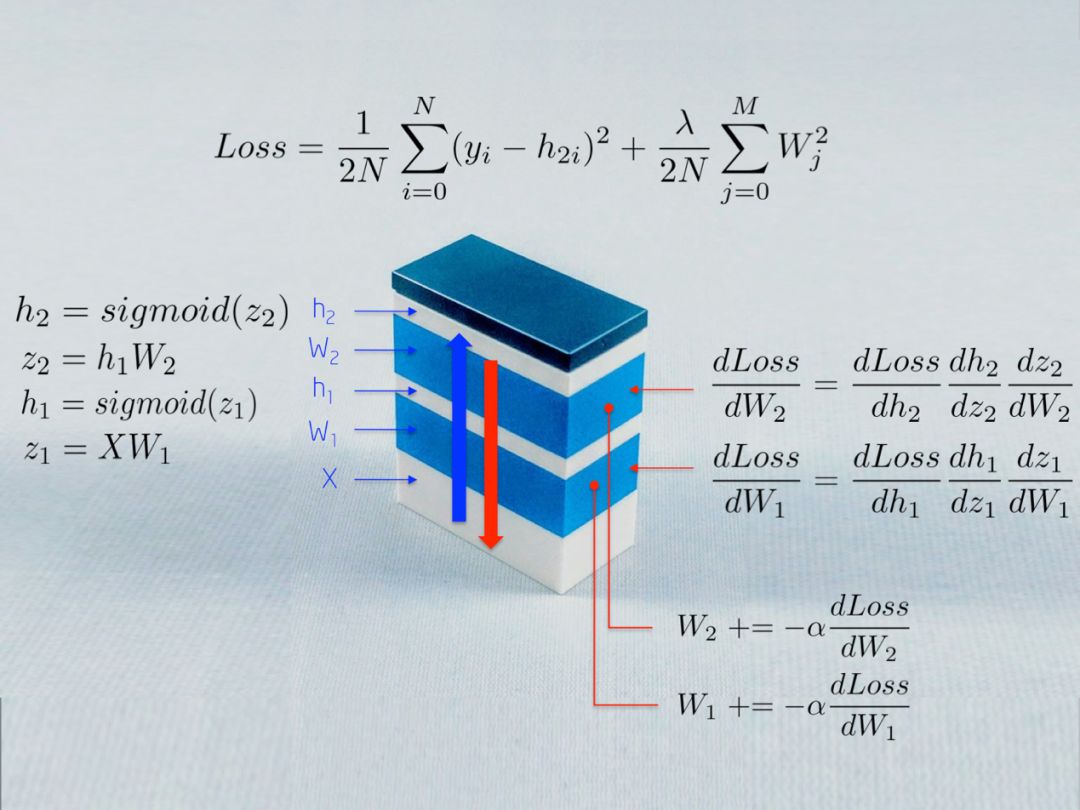
上图描述了一些用于训练神经网络的数学公式。在本文中，我们将对此进行解释。读者可能会发现有趣的是，神经网络是一堆具有不同目的的模块组合连接而成。

为什么要阅读这篇文档

如果你理解了神经网络的内部构成，你将很快知道当模型不起作用时，首先要改变什么，并定义一个策略来测试你所知道的算法中的不变量和的预期行为。当你想要在您使用的ML库中创建并实现新的功能时，这也会很有帮助。

因为调试机器学习模型是一项复杂的任务。根据经验，第一次尝试时，数学模型并不像预期的那样工作。它们可能会对新数据的准确性较低，使你花费较长的训练时间或过多的内存，返回大量错误的值或NaN，等等。当你知道这些算法是如何工作的时候，会变得很方便，比如:

如果训练时间太长，那么增加minibatch的大小来减小观测值的方差，从而帮助算法收敛，这可能是一个好主意
如果你得到的预测值为NaN，该算法可能梯度过大，从而导致内存溢出。把它看作是经过多次迭代后的连续矩阵乘法。降低学习率会降低这些值。减少层数将减少乘法的数量。Clippinggradients将显式地控制这个问题。

具体例子:学习XOR函数

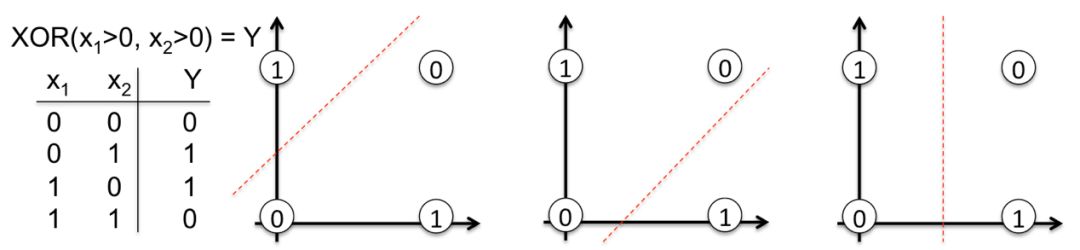
让我们打开黑盒子。现在我们将从头构建一个学习XOR函数的神经网络。这种非线性函数的选择绝不是随机的。如果没有反向传播，就很难学会用一条直线来分隔类。

为了说明这个重要的概念，请仔细看下图，一条直线是如何不能将XOR函数的输出0和1分开的。现实生活中的很多问题也是非线性可分的。

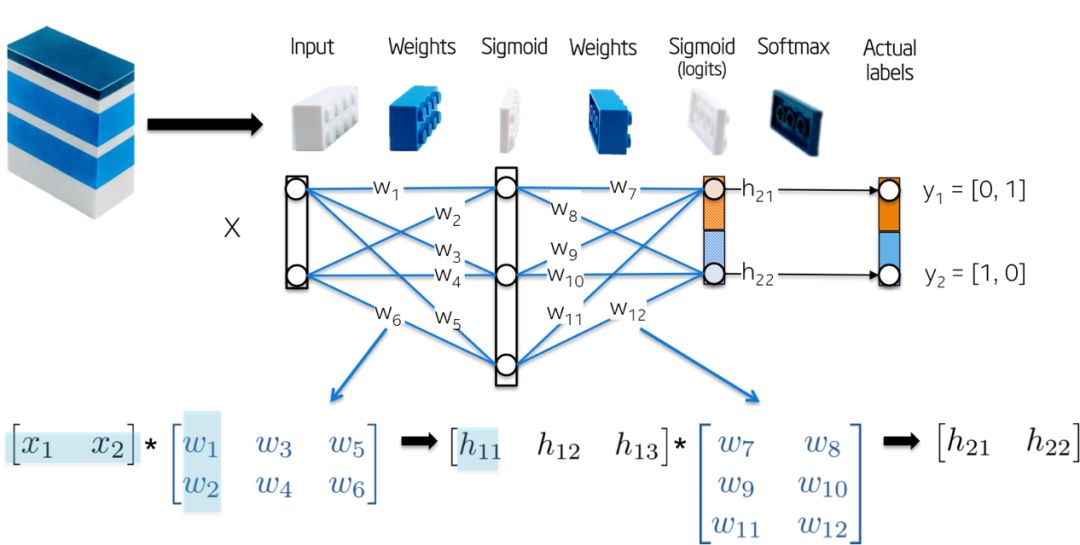
网络拓扑结构是很简单的，

-输入X是一个二维向量;

-权重W1是一个具有随机初始化值的2x3矩阵;

-隐含层h1由三个神经元组成。每个神经元接受一个加权的观测值作为输入，这是下图中绿色高亮显示的内积:z1 = [x1, x2][w1, w2];

-权重W2是一个具有随机初始化值的3x2矩阵;

-输出层h2由两个神经元组成，因为XOR函数返回0(y1=[0,1])或1 (y2 =[1,0]);

更直观地如下图:

现在我们来训练模型。在我们的简单示例中，可训练的参数是权重，但请注意，目前的研究正在探索更多类型的参数进行优化。例如层之间的shortcut、正则化分布、拓扑结构、残差、学习率等。

反向传播是一种向(梯度)方向更新权值的方法，它在给定一批标记的观测值的情况下最小化一个预先定义的误差度量(称为损失函数)。它是一种更通用的技术的特例，这种技术称为逆向累加模式下的自动微分（automatic differentiation in reverse accumulation mode）。

网络初始化Network Initialization

让我们用随机数初始化网络权重。

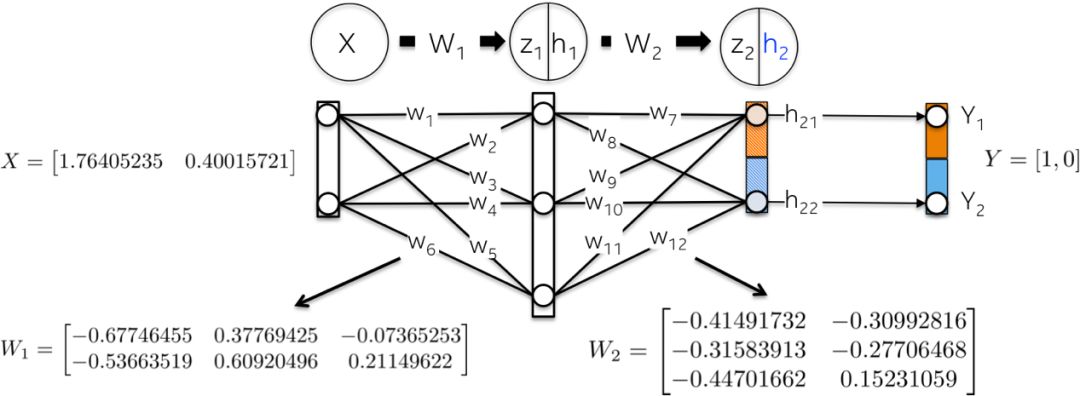
前向步骤Forward Step

这一步的目标是将输入X向前传播到网络的每一层，直到计算输出层h2中的向量为止。

步骤如下：

-以权值W1为kernel，线性映射输入数据X:

-使用Sigmoid函数缩放这个加权和z1，以获得第一个隐藏层h1的值。注意，原来的2维向量现在映射到3维度空间;

-第二层h2也发生了类似的过程。我们先计算第一个隐层的加权和z2，它现在是输入数据;

-然后计算它们的Sigmoid激活函数。这个向量 [0.37166596 0.45414264]表示给定输入X的网络计算的对数概率或预测向量;

计算损失Computing the Total Loss

请注意，损失函数包含一个正则化组件，该组件会像Ridge回归那样惩罚较大的权重值。换句话说，换句话说，较大的平方权重值将增加损失函数，这是我们确实想要最小化的误差度量。

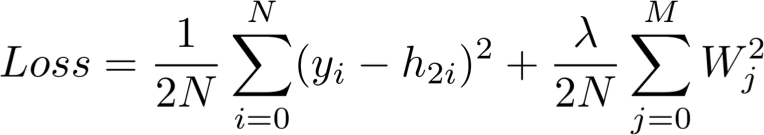
反向步骤Backward step

这个步骤的顺序是向后的，而不是向前的。首先计算损失函数对输出层权重的偏导数(dLoss/dW2)，然后计算隐含层的偏导数(dLoss/dW1)。

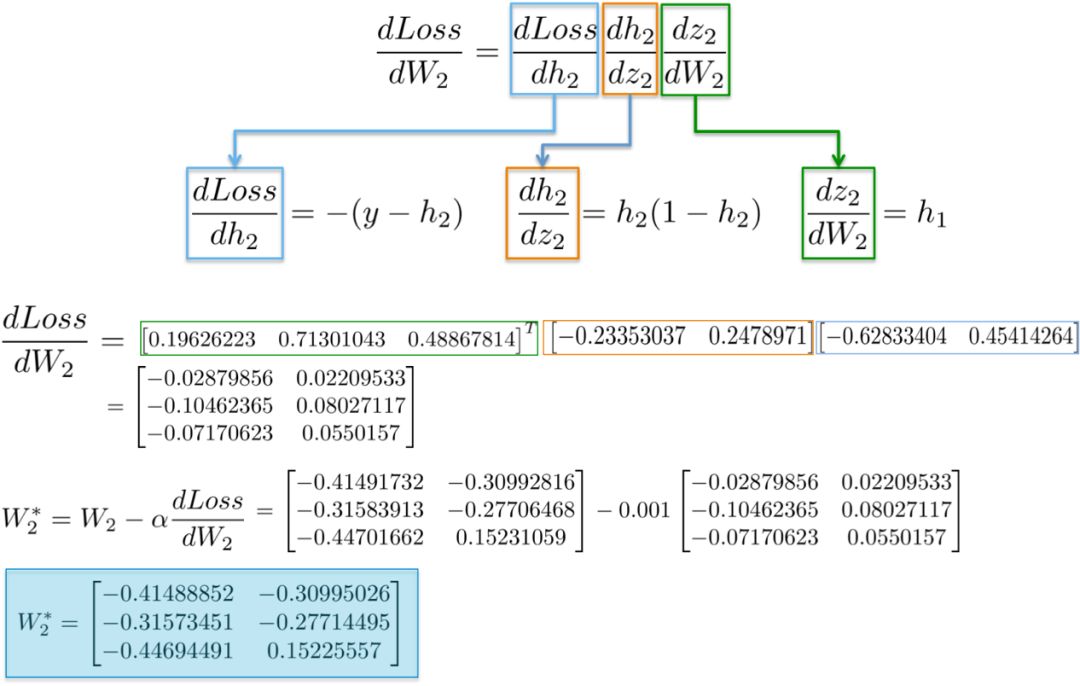
(i) dLoss/dW2

链式法则表明，我们可以将神经网络的梯度计算分解为可微的部分：

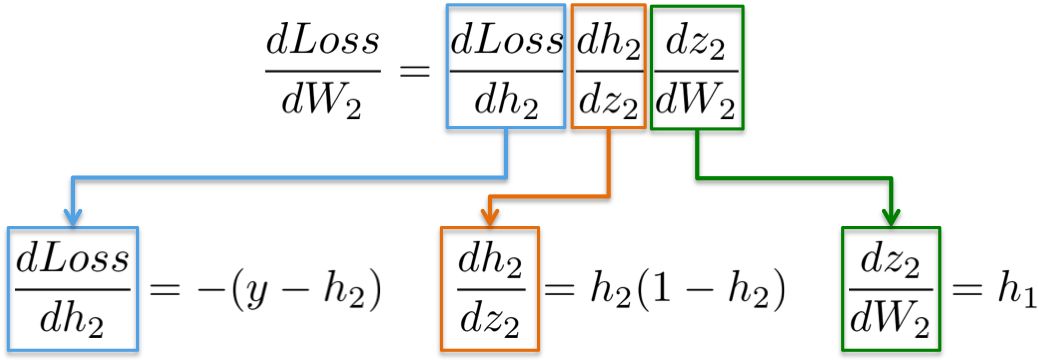
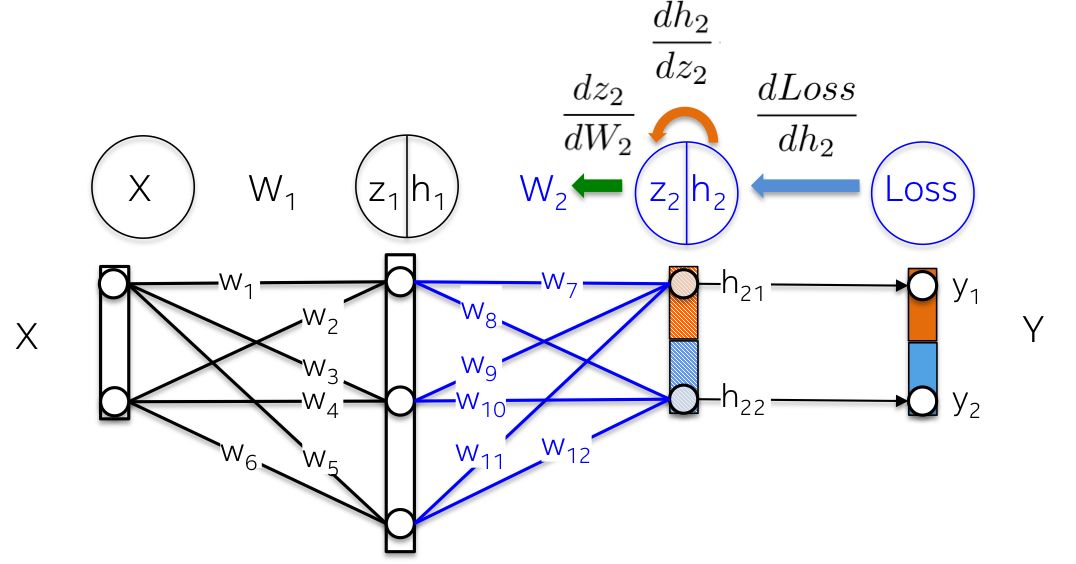
更直观地说，我们的目标是更新下图中的权重W2（蓝色）。为此，我们需要计算沿着链的三个偏导数。

将值代入这些偏导数中，我们就可以计算出关于权值W2的梯度，如下所示。

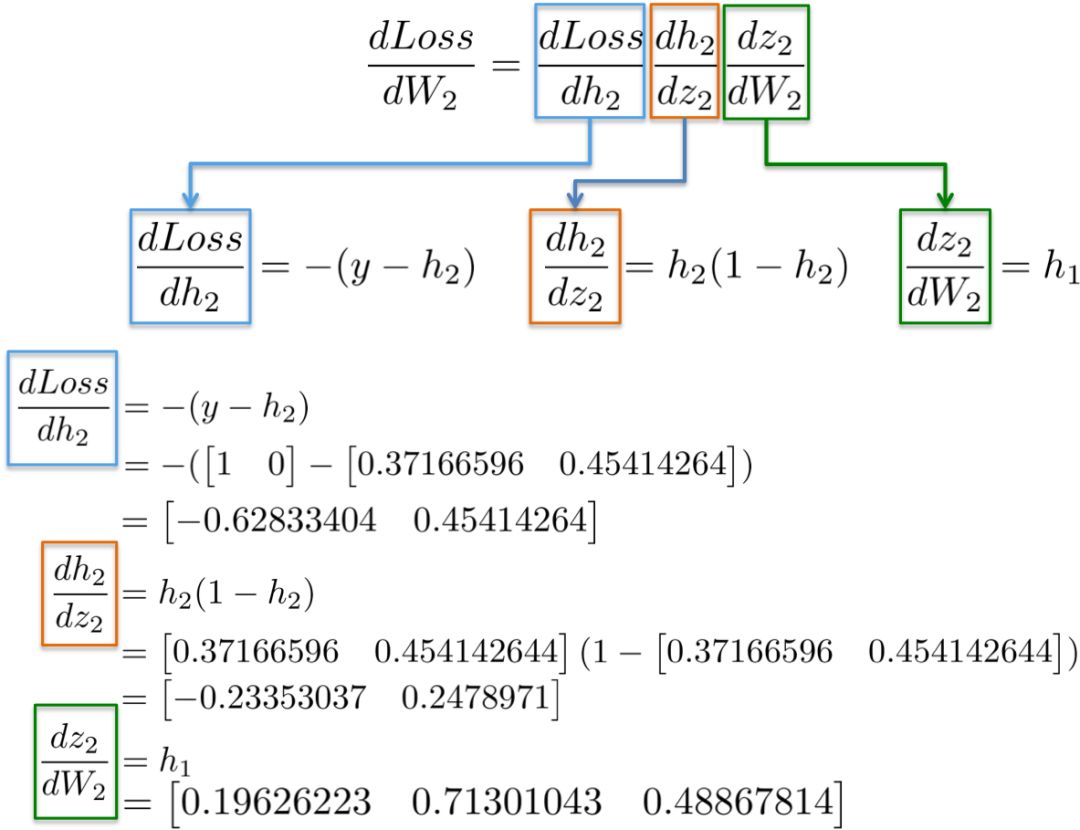
结果是一个3x2矩阵dLoss/dW2，它将按照最小化损失函数的方向更新原始的W2值。

(ii) dLoss/dW1

计算用于更新第一个隐藏层W1的权重的链式法则显示了重用现有计算的可能性。

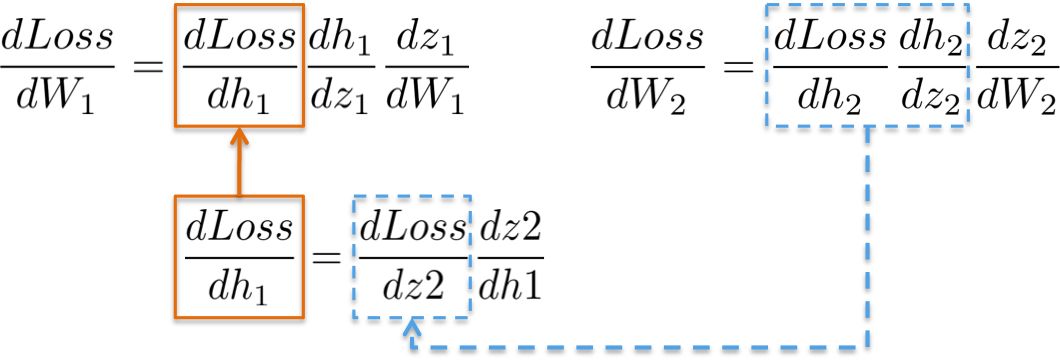
更直观地说，从输出层到权值W1的路径涉及到已经在后一层计算过的偏导数。

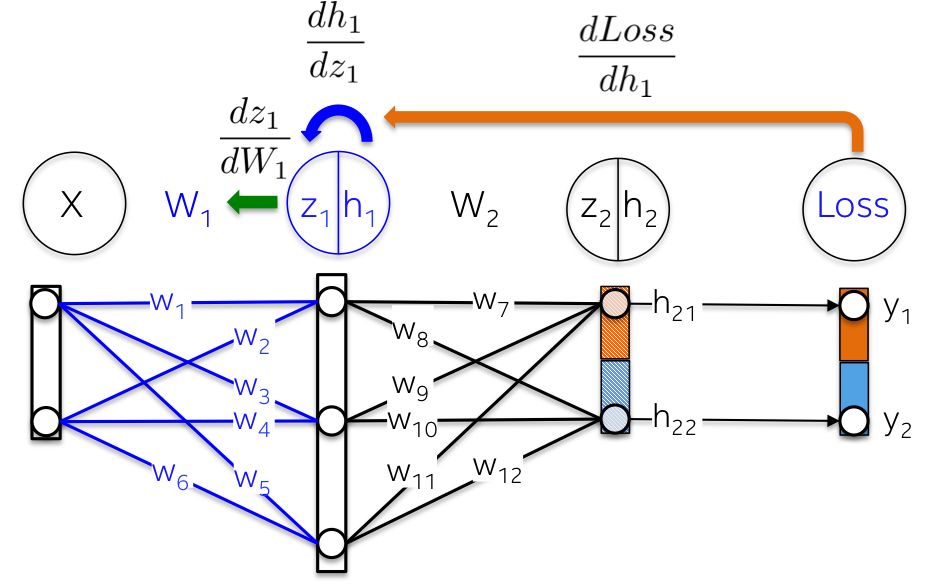
例如，偏导数dLoss/dh2和dh2/dz2在上一节中已经被计算为输出层dLoss/dW2学习权重的依赖项。

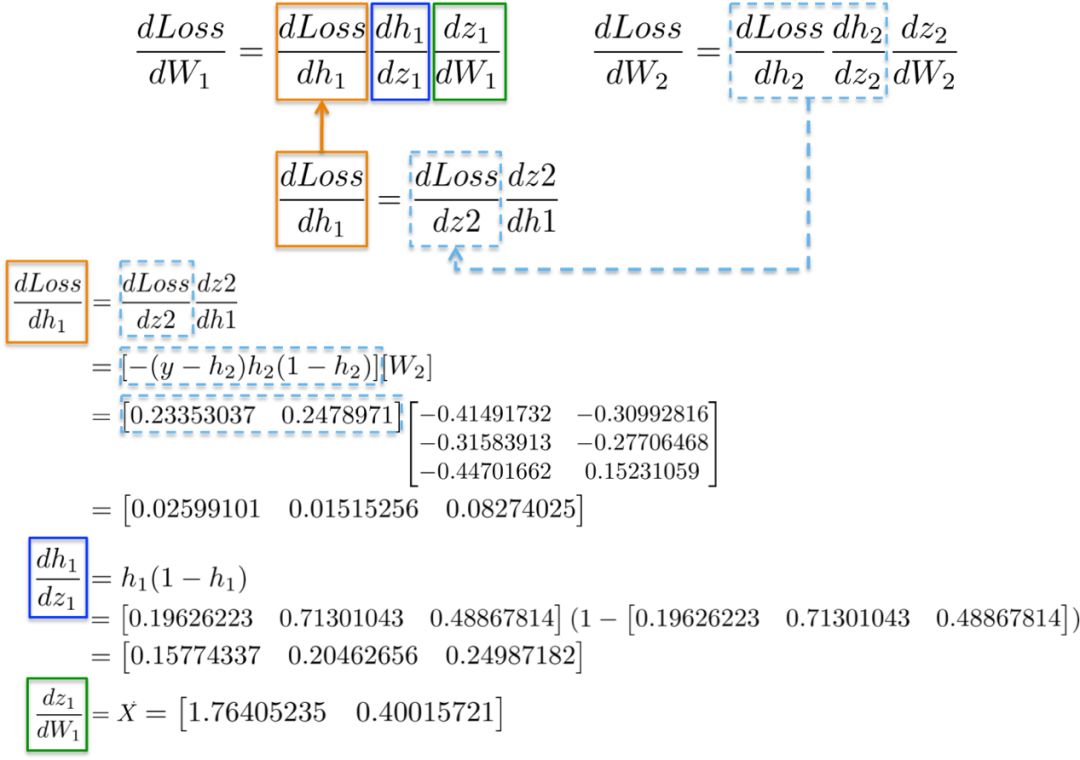
将所有的导数放在一起，我们可以再次执行链式法则来更新隐藏层W1的权值:

最后，我们分配了新的权重值，并完成了网络训练的迭代。

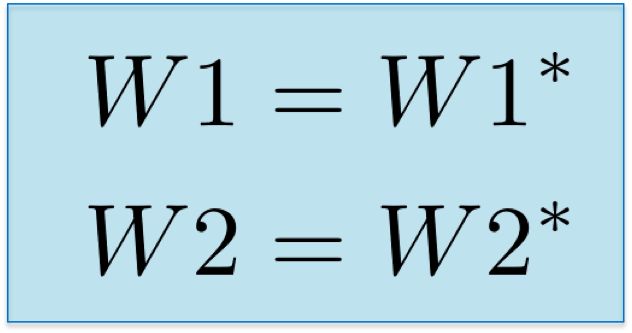
实现Implementation

让我们将上面的数学方程转换成仅使用Numpy作为线性代数引擎的代码。神经网络是在一个loop中训练的，在这个loop中，每次迭代都向网络提供已校准的输入数据。在这个小示例中，我们只考虑每次迭代中的整个数据集。由于我们在每个loop中都用相应的梯度(矩阵dL_dw1和dL_dw2)更新可训练参数(代码中的矩阵w1和w2)，因此对前向传播、损失函数和反向传播的计算具有良好的泛化性。代码在这个repository中:https://github.com/omar-florez/scratch_mlp

Let's Run This!让我们来运行这个模型

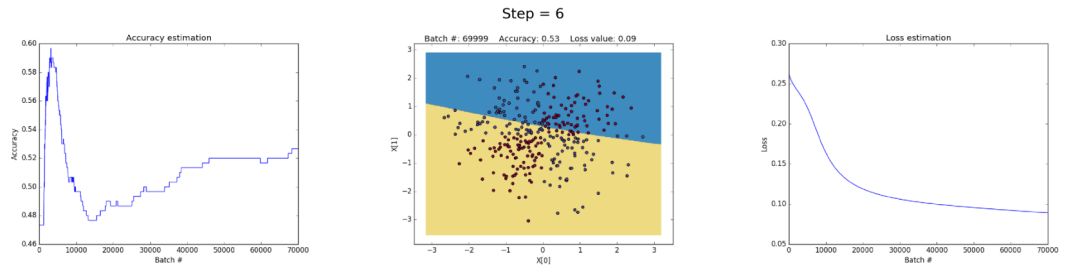
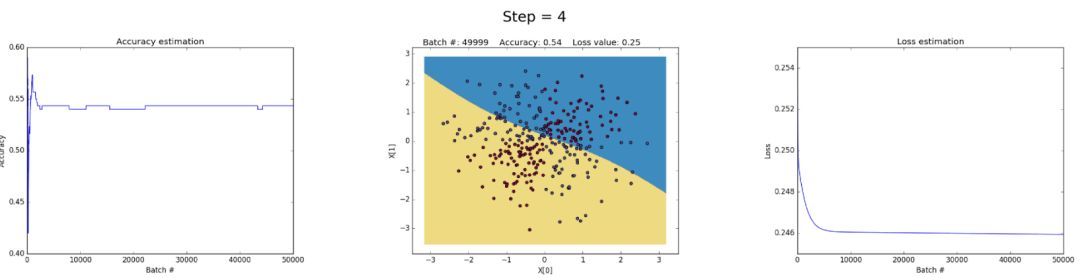
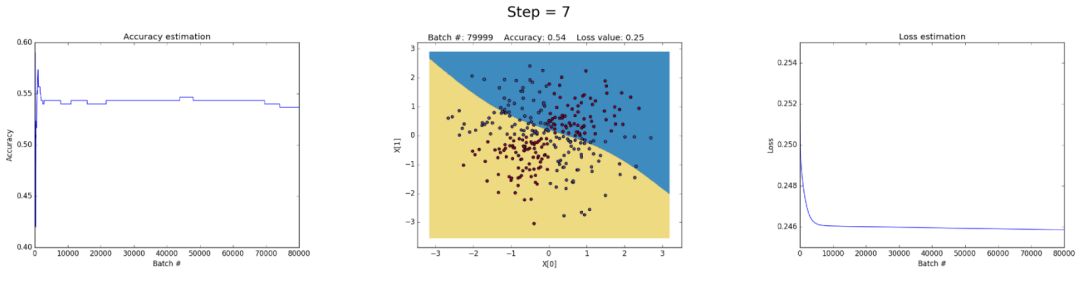
下面是一些经过训练的神经网络，它们可以在多次迭代中逼近XOR函数。

左图：Accuracy。中心图：Learned decision boundary。右图：Loss function。

首先，让我们看看隐藏层中有3个神经元的神经网络是如何具有small capacity的。该模型学习用一个简单的决策边界将两个类分开，该边界开始是一条直线，然后显示非线性行为。随着训练的继续，在正确的情况下，损失函数会很好地降低。

在隐层中有50个神经元可以显著提高模型学习更复杂决策边界的能力。这不仅可以产生更精确的结果，而且还可以利用梯度，这是训练神经网络时一个值得注意的问题。当非常大的梯度在反向传播过程中乘以权重，从而生成较大的更新权重时，就会发生这种情况。这就是为什么在训练的最后一步(step> 90)损失值突然增加的原因。损失函数的正则化部分计算的权重的平方值(sum(W²)/2N) 已经非常大了。