BAT码农的刷题日记01——高效面试算法题 | 逆序数为K的排列数量 629. K Inverse Pairs Array

高效面试算法题 | 逆序数为K的排列数量 629. K Inverse Pairs Array

=====================================

【导读】主题链路知识是我们专知的核心功能之一，为用户提供AI领域系统性的知识学习服务，一站式学习人工智能的知识，包含人工智能（ 机器学习、自然语言处理、计算机视觉等）、大数据、编程语言、系统架构。使用请访问专知进行主题搜索查看 - 桌面电脑访问www.zhuanzhi.ai,  手机端访问www.zhuanzhi.ai 或关注微信公众号后台回复"专知"进入专知，搜索主题查看。Leetcode刷题是应届生找工作必备，我们专知平台专门邀请腾讯资深工程师老徐，从今天开始，定期把刷题经验分享给大家，希望大家喜欢。

专栏介绍:

BAT码农一枚。在校时未参加过OI/ACM赛事，算法能力一般。毕业后参加Google面试，作为挂在HC轮，遂决心通过米企社招肉身翻墙，在LC上陆续刷题一年，在这里和大家分享准备面试和刷题的经验。

问题

https://leetcode.com/problems/k-inverse-pairs-array/description/

Given two integers n and k, find how many different arrays consist of numbers from 1 to n such that there are exactly k inverse pairs.

We define an inverse pair as following: For ith and jth element in the array, if i < j and a[i] > a[j] then it’s an inverse pair; Otherwise, it’s not.

Since the answer may be very large, the answer should be modulo 109 + 7.

Example 1:

Input: n = 3, k = 0

Output: 1

Explanation:

Only the array [1,2,3] which consists of numbers from 1 to 3 has exactly 0 inverse pair.

Example 2:

Input: n = 3, k = 1

Output: 2

Explanation:

The array [1,3,2] and [2,1,3] have exactly 1 inverse pair.

问题描述

给出自然数1…n（n<=1000）,求对这些数进行排列后，满足逆序对数量为k的排列数量。

**逆序对的定义：**在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序对。

逆序对数量的一般计算方式:
针对一个排列Serial=a1,a2,a3…an，排列中的第i个元素是ai，如果ai后续的元素ai+1,ai+2…an中存在ki个元素比ai小，则ai和这ki个元素构成了ki个逆序对。对所有n个元素对应的逆序对数量ki求和，得到排列Serial的逆序对数量：。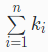

最小逆序对数量: 顺序排列1,2,3…n，逆序数为0，因为不存在排在前面的数大于后面的数。

最大逆序对数量:
逆序排列n,n-1,n-2…1，因为任取排列中的第i个元素，和后面的(n-i)个元素，每个都构成逆序对，ki取最大值n-i,总逆序对数量为。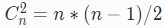

解决思路

---

思路一.DFS

题目希望我们找到长度为N逆序数为K的排列的数量。

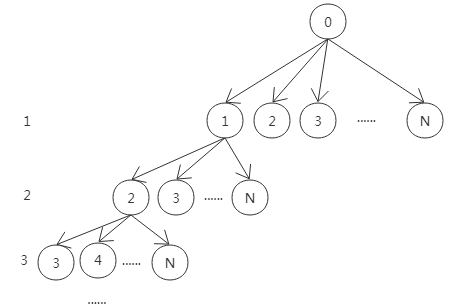
最直观的方法是枚举所有可能的排列。采用dfs深搜算法，搜到第i层的时候，从元素1…n中取尚未访问过的元素ai，逆序数减少ki；当逆序数减少为0后，对排列计数增加1并回溯。

Dfs 深搜示意图

这种方法的问题是需要枚举所有可能的排列，时间复杂度接近N！，即使做了适当的剪枝策略，依然会超时。

思路二.DP：

设长度为i逆序对为j的排列数量为re[i][j]。

对长度为i逆序对为j的排列，枚举发现排列的首元素a1的可能取值为1,2,3…i,分别会和排列的后续元素a2…ai生成0,1,2…i-1个逆序对，则后续子排列a2,a3…ai的逆序对数分别为j,j-1,j-2…j-(i-1),对应的排列数量分别为re[i-1][j],re[i-1][j-1],re[i-1][j-2]…re[i-1][j-(i-1)]。显然，re[i][j]是re[i-1][j],re[i-1][j-1],re[i-1][j-2]…re[i-1][j-(i-1)]之和。

于是可以得到状态转移方程:

re[i][j] = re[i-1][j] + re[i-1][j-1] + re[i-1][j-2] + … +re[i-1][j - i + 1]

上述算法需要计算所有re[i][j]，对每个re[i][j]，计算时间复杂度为O(k), 所以总体计算时间复杂度为O（n*k2）。

但是提交之后依旧超时，说明状态转移放方程可以进一步优化。

思路三.优化DP

观察上述DP的转移方程:

re[i][j-1] = re[i-1][j-1] + re[i-1][j-2] + …+re[i-1][j - i + 1] + re[i-1][j-1- i + 1]

re[i][j] = re[i-1][j] + re[i-1][j-1] + re[i-1][j-2] + … +re[i-1][j - i + 1]

发现规律:

re[i][j]-re[i][j-1]=re[i-1][j] - re[i-1][j-1-i+i]

可以推导出新转移方程:

re[i][j] = re[i][j-1] + re[i-1][j] - re[i-1][j-1-i+i] (当j-i>=0时)

新的转移方程应用之后，对每个re[i][j]的计算时间复杂度降低为O(1)，总体时间复杂度降低为O(nk).

Runtime: 19 ms

以上就是老徐关于这道题的总结经验，希望大家能够理解，有什么问题可以在我们的专知公众号平台上交流或者加我们的QQ专知-人工智能交流群 426491390，也可以加入专知——Leetcode刷题交流群（请先加微信小助手weixinhao: Rancho_Fang）。
同时请，关注我们的公众号，获取最新关于专知以及人工智能的资讯、技术、算法等内容。扫一扫下方关注我们的微信公众号。