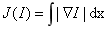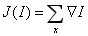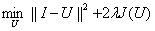【干货】计算机视觉实战系列08——用Python做图像处理- 专知

会员服务 ·

【干货】计算机视觉实战系列08——用Python做图像处理

Hui

【导读】在前面几讲中，专知成员Hui介绍了PIL、Matplotlib、Numpy、SciPy等Python图像处理的工具包。这一讲中，我们将介绍一个具体的实例——图像去噪，作为前面几讲的总结。

【干货】计算机视觉实战系列01——用Python做图像处理（基本的图像操作和处理）

【干货】计算机视觉实战系列02——用Python做图像处理（Matplotlib基本的图像操作和处理）

【干货】计算机视觉实战系列03——用Python做图像处理（Numpy基本操作和图像灰度变换）

【干货】计算机视觉实战系列04——用Python做图像处理（图像的缩放、均匀操作和直方图均衡化）

【干货】计算机视觉实战系列05——用Python做图像处理（主成分分析）

【干货】计算机视觉实战系列06——用Python做图像处理（图像高斯模糊分析）

【干货】计算机视觉实战系列07——用Python做图像处理（SciPy库的应用——图像导数实战）

图像去噪

图像去噪是给定一幅受损图像，在去除图像噪声的同时，尽可能地保留图像细节和结构的处理技术。图像去噪对于很多应用来说都非常重要；这些应用范围很广，小到让你的照片看起来更漂亮，大到提高卫星图像的质量。我们这里使用ROF去噪模型，ROF模型具有很好的性质；使处理后的图像更加平滑，同时保留图像边缘和结构信息。

ROF模型的数学基础和处理技巧非常高深，有兴趣的读者可以自学深入了解，本文只是做一个简单介绍。

ROF模型

一副图像I的全变差（Total Variation,TV）定义为梯度范数之和。

在连续表示的情况下，全变差表示为：

在离散表示的情况下，全变差表示为：

其中，上面的式子是在所有图像坐标x=[x,y]上取和。

在ROF模型里，目标函数是为了寻找降噪后的图像U，使下式最小：

其中范数||I-U||是去噪后图像U和原始图像I差异的度量。也就是说，本质上该模型使去噪后的图像像素值“平坦变化”，但是在图像区域的边缘上，允许图像像素值“跳跃变化”。

代码

from numpy import *
from numpy import linalg as LA
from numpy import random
from scipy.ndimage import filters
from scipy.misc import imsave
from PIL import Image


def denoise(im, U_init, tolerance=0.1, tau=0.125, tv_weight=100):
    m, n = im.shape  # 噪声图像的大小
    U = U_init
    Px = im  # 对偶域的x 分量
    Py = im  # 对偶域的y 分量
    error = 1

    while (error > tolerance):
        Uold = U

        # 原始变量的梯度
        GradUx = roll(U, -1, axis=1) - U  # 变量U 梯度的x 分量
        GradUy = roll(U, -1, axis=0) - U  # 变量U 梯度的y 分量

        # 更新对偶变量  
        PxNew = Px + (tau / tv_weight) * GradUx
        PyNew = Py + (tau / tv_weight) * GradUy
        NormNew = maximum(1, sqrt(PxNew ** 2 + PyNew ** 2))

        Px = PxNew / NormNew  # 更新x 分量（对偶）
        Py = PyNew / NormNew  # 更新y 分量（对偶）

        # 更新原始变量
        RxPx = roll(Px, 1, axis=1)
        RyPy = roll(Py, 1, axis=0)

        DivP = (Px - RxPx) + (Py - RyPy)  # 对偶域的散度
        U = im + tv_weight * DivP  # 更新原始变量

        # 更新误差
        error = linalg.norm(U - Uold) / sqrt(n * m)
    return U, im - U


im = zeros((500, 500))
im[100:400, 100:400] = 128
im[200:300, 200:300] = 255
im = im + 30 * random.standard_normal((500, 500))

U, T = denoise(im, im)
G = filters.gaussian_filter(im, 10)

from scipy.misc import imsave

imsave('test1.pdf', U)
imsave('test2.pdf', G)

输出结果如下：

（a）

（b）

图中（a）为经过高斯模糊的图像，（b）为经过ROF模型去噪后的图像

在上面代码中，输入为含有噪声的灰度图像、U 的初始值、TV 正则项权值、步长、停业条件；输出：去噪和去除纹理后的图像、纹理残留。im.shape表示噪声图像的大小；Px和Py分别表示对偶域的x分量和对偶域的y分量；GtandUx和GrandUy分别表示变量U梯度的x分量和y分量； RxPx = roll(Px,1,axis=1)和 RyPy = roll(Py,1,axis=0)分别表示对x 分量进行向右x 轴平移和对y 分量进行向右y 轴平移；denoise方法最终返回去早后的图像和纹理残余。

在这个例子中，我们使用了roll() 函数。顾名思义，在一个坐标轴上，它循环“滚动”数组中的元素值。该函数可以非常方便地计算邻域元素的差异，比如这里的导数。我们还使用了linalg.norm() 函数，该函数可以衡量两个数组间（这个例子中是指图像矩阵U 和Uold）的差异。

下面，我们使用Erza Scarlet的图像进行去噪的实战练习

代码如下：

from numpy import *
from numpy import linalg as LA
from numpy import random
from scipy.ndimage import filters
from scipy.misc import imsave
from PIL import Image
import matplotlib.pyplot as plt


def denoise(im, U_init, tolerance=0.1, tau=0.125, tv_weight=100):
    m, n = im.shape  # 噪声图像的大小
    U = U_init
    Px = im  # 对偶域的x 分量
    Py = im  # 对偶域的y 分量
    error = 1

    while (error > tolerance):
        Uold = U

        GradUx = roll(U, -1, axis=1) - U  # 变量U 梯度的x 分量
        GradUy = roll(U, -1, axis=0) - U  # 变量U 梯度的y 分量

        PxNew = Px + (tau / tv_weight) * GradUx
        PyNew = Py + (tau / tv_weight) * GradUy
        NormNew = maximum(1, sqrt(PxNew ** 2 + PyNew ** 2))

        Px = PxNew / NormNew  # 更新x 分量（对偶）
        Py = PyNew / NormNew  # 更新y 分量（对偶）

        RxPx = roll(Px, 1, axis=1)  # 对x 分量进行向右x 轴平移
        RyPy = roll(Py, 1, axis=0)  # 对y 分量进行向右y 轴平移

        DivP = (Px - RxPx) + (Py - RyPy)  # 对偶域的散度
        U = im + tv_weight * DivP  # 更新原始变量

        # 更新误差
        error = linalg.norm(U - Uold) / sqrt(n * m)
    return U, im - U


fig = plt.figure(figsize=(15, 15))
im = array(Image.open('test.jpg').convert('L'))
U, T = denoise(im, im)
plt.imshow(U, plt.cm.gray)
plt.axis('equal')
plt.axis("off")
plt.show()