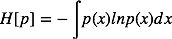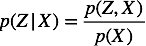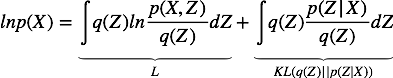【深度】专知主题链路知识推荐#8-机器学习中的变分推断方法(Variational Inference)简介01
^_^点击上方“专知”关注获取更多AI知识!
【导读】主题链路知识是我们专知的核心功能之一,为用户提供AI领域系统性的知识学习服务,一站式学习人工智能的知识,包含人工智能( 机器学习、自然语言处理、计算机视觉等)、大数据、编程语言、系统架构。使用请访问专知 进行主题搜索查看 - 桌面电脑访问www.zhuanzhi.ai, 手机端访问www.zhuanzhi.ai 或关注微信公众号后台回复" 专知"进入专知,搜索主题查看。今天给大家继续介绍我们独家整理的机器学习——机器学习中的变分推断方法(Variational Inference)简介。
今天的变分推断专题邀请到中科院自动化研究所博士生ylfzr同学来分享他关于机器学习中变分推断方法的简介教程,这一部分理论由于图模型和变分自编码器等等也变得越来越重要,计划推出一系列关于变分推断方法的教程,敬请期待!
1、变分推断方法简介
变分方法起源于18世纪的欧拉、拉格朗日等的研究(calulus of variations)。它可以看作是对标准微积分的扩展。标准微积分关注寻找函数的导数, 我们常常利用一阶优化条件(1st order optimal condition),即在该点处导数为零来寻找函数的极值。 注意此时我们寻找的最优点(optimal point)一般来讲是实数空间内的一个点。我们可以将函数想象为一个映射,这个映射以一个变量的值作为输入,返回函数值作为输出。类似地,我们定义泛函(functional)作为一个映射,它以一个函数作为输入,返回泛函的值作为输出。一个例子是熵H[p],它的输入是一个概率分布p(x),如公式(1)所示:
在概率推理中,我们经常需要优化的量是一个泛函。研究所有可能的输入函数,找到最大化或者最小化泛函的函数就是问题的解。变分推理,即是在所有可能的概率分布中,找到最优的来近似我们所需要的部分(通常是后验概率)。通常情况下变分推理问题会被转化成为优化问题,可以使用常规的高效优化求解器求解。因此相比其他的技术如蒙特卡洛马尔科夫链(MCMC)采样更适用于大规模数据的应用场景,想学习蒙特卡洛马尔科夫链完整教程,请看专知推出的马尔科夫链蒙特卡洛采样入门教程。
变分推断方法最早借鉴了统计物理的研究方法。1987年,Peterson 和 Anderson 首次使用了均值场(mean field) 来求解神经网络。90年代早期, Micheal Jordan的研究组将其拓展到多种统计模型中。
几乎与此同时,Neal 和 Hinton 将变分推断与EM算法联系起来,大大推动了该方法的发展。该方法开始应用于一些复杂模型比如mixture of experts, HMM 等。在机器学习大牛Micheal Jordan, Zoubin Ghahramani, David Blei, Max Welling等的推动下,变分方法已经广泛被运用于各个领域中:概率编程, 强化学习,深度学习等等, 成为了解决或解释机器学习问题很有力的工具。
2、贝叶斯学习中的变分推断方法
由于变分推断主要运用于贝叶斯学习的场景下,我们首先简单介绍贝叶斯学习,引入变分推断方法,并且最后给出一个采用变分推理方法求解传统共轭模型的简单例子(这部分会在变分推断方法简介02中推出):变分方法求解一元高斯。以后我们会介绍非共轭模型的求解并给出一个例子: 变分自编码器VAE(variational autoencoder)的求解。
2.1 贝叶斯学习
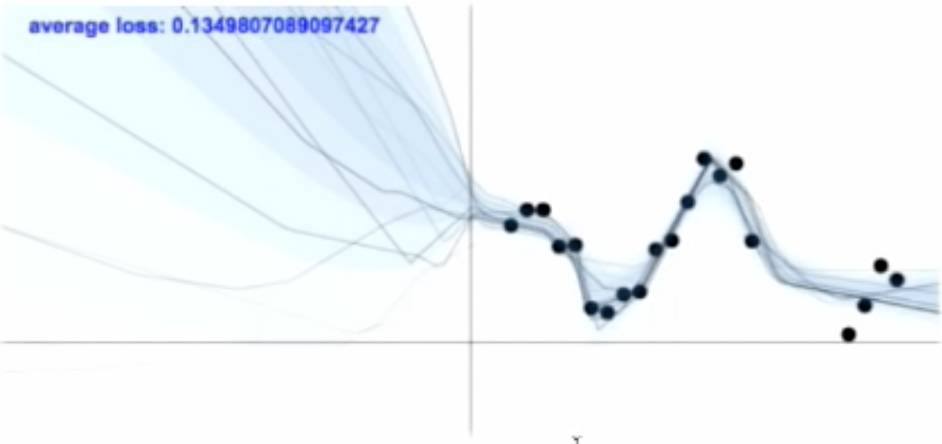
我们已经知道我们常见的大多数学习问题的核心是模型的参数估计,通过最大似然(MLE)或最大后验概率(MAP)估计我们可以得到当前模型的较好的参数,由于一组参数对应参数空间的一个点, 这类估计方法又被称为“点估计”。然而当我们使用点估计去完成一定的任务时, 常常会遇到一些问题, 比如模型过拟合,比如模型在数据稀疏时候表现不佳等。其原因之一就是我们太过于“确信”我们学到的模型。下图可以给我们一个直观的感受。
图: 回归模型中的不确定性[4]
如上图所示, 在纵轴的右侧我们有较多的数据点,因此我们可以得到较好的模型估计来拟合数据。 在这个区域,我们相信我们得到的模型有较好的表现。(蓝色区域颜色的深浅显示了我们模型的确信程度或“方差”) 而在纵轴的左侧,几乎没有任何数据点,在这一区域,任何一个“点估计”(对应一条拟合曲线)很大可能性都会给出错误的预测结果。我们说,系统并不能确定在该区域的预测值, 任何 “鲁莽”的预测行为都是不可靠的。 那么,如何才能让我们学习的系统知道它此时并不能给出合适的预测呢?我们可以将对模型(参数)的信念(Belif)加入到学习中:我们将模型中的参数扩展为随机变量,其方差就代表了模型对当前的参数的不确定性。这就是之前我们讲到过的贝叶斯估计。具体可以查看专知推出的机器学习中的贝叶斯参数估计。
2.2 变分推断
贝叶斯估计的核心任务是在给定观测数据 X 的条件下,计算隐含变量 Z 的后验分布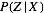
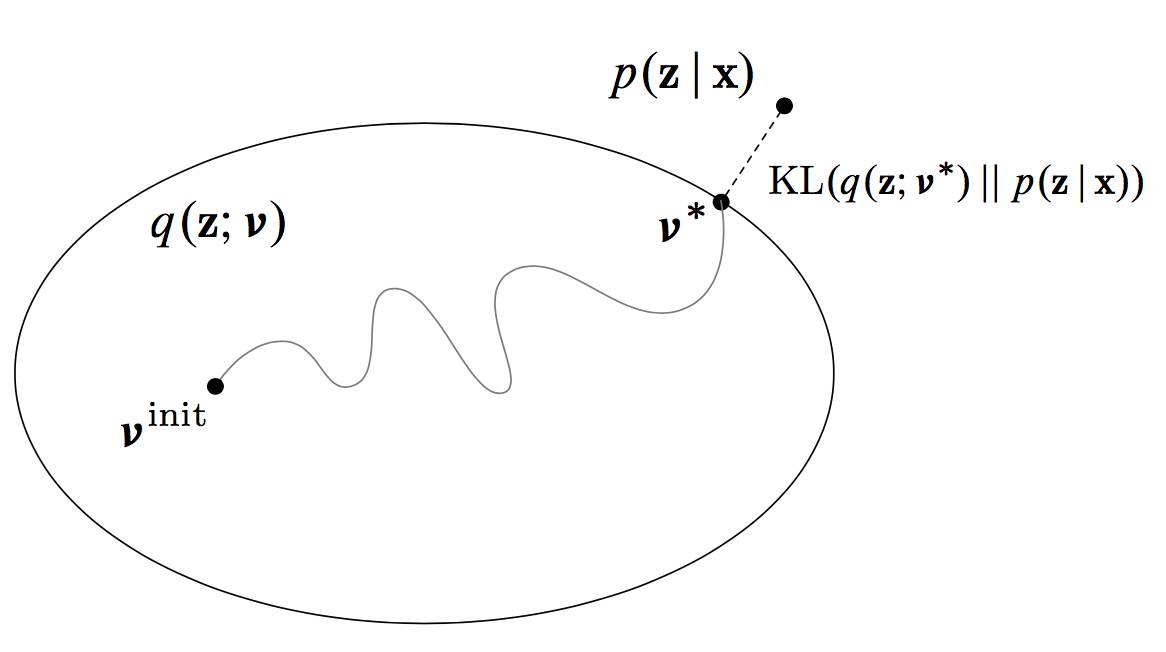
当精确的推理不可行时,我们转而希望获得一个近似的结果。我们假设一个容易的分布形式来替代精确的后验分布,逐步迭代优化使得二者尽量接近,这就是最基本的近似变分推理的想法。
下面我们开始具体解释变分推断的工作过程。
首先定义联合概率分布我们就可以得到一个概率模型: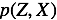
对未知变量的推理即在观测数据的基础上更新隐含变量的后验,如公式(2)所示:
类似于最大似然估计,我们仍然希望在我们学习到的模型可以最大可能地产生出我们的观测样本, 即最大化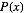
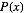
其中,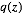

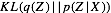
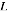
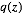

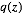
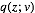
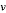
图: 变分推理示意
对于变分推断如何求解以及如何应用,敬请期待后续的教程!
参考资料
[1] C.Bishop “Pattern Recognition and Machine Learning” 2006
[2] D.Blei A.Ng M. Jordan Latent Dirichlet Allocation[M]. JMLR.org, 2003.
[3] Y.Gal Uncertainty in Deep Learning 2016
[4] 徐亦达 Statistical Notes
http://www-staff.it.uts.edu.au/~ydxu/statistics.htm
[5] NIPS 2016 tutorial: Variational Inference: Foundations and Morden Methods
上面就是关于机器学习中变分推断方法的一个简介,后续会不断推出它的一系列应用教程,原创不易,请多多支持,有什么问题可以在我们的专知公众号平台上交流或者加我们的专知-人工智能交流群 426491390
欢迎使用专知-一体化AI知识服务!点击阅读原文即可访问,访问专知,获取更多人工智能最新资讯、技术、算法、知识等资源。
同时请,关注我们的公众号,获取最新关于专知以及人工智能的资讯、技术、算法等内容。扫一扫下方关注我们的微信公众号。