【论文笔记】Graph U-Nets- 专知

【论文笔记】Graph U-Nets

【导读】卷积神经网络可以在图像（image）上随意操作，并且像U-Nets这种编码-解码框架已经成功地应用在许多图像像素级预测任务中，但是在图(graph)数据上具有很大的挑战。为了解决这些挑战，我们提出了一个新颖的图池化（gPool）和图上采样（(gUnpool)）操作。图池化层（gPool）根据节点在可训练投影向量上的标量投影值，自适应地选择一些节点形成较小的图。我们也提出了gUnpool层作为gPool的反操作，利用在相应的gPool层中选择的节点的位置信息，将图恢复到原来的结构中。并且基于我们提出的gPool层与gUnpool层，我们提出了一个在图上的编码-解码模型，称为图U-Nets。在节点分类以及图分类任务中取得比以前的模型更好的性能。

https://arxiv.org/pdf/1905.05178.pdf

动机

由于图上的节点没有位置信息，故进行编码的池化操作与进行解码的上采样操作在图数据中无法使用，进而无法在图数据上使用U-Net等解码-编码框架。基于此，我们提出了一个新颖的图池化（gPool）和图上采样（(gUnpool)）操作，并且基于gPool层与gUnpool层，我们提出了一个在图上的编码-解码模型，称为图U-Nets，在对高级特征进行编码和解码同时保存本地空间信息。

Graph U-Nets

图池化层

由于图上的节点没有位置信息，故先前的池化操作（最大池化、平均池化）不能在图上使用。基于此，我们提出了图池化层(gPool)可以在图上进行下采样。在这一层，我们自适应的选择一个节点子集去形成一个新的并且更小的图。

我们利用一个可训练的投影向量p，通过将所有节点特征投影到1维，我们可以利用k-max池化进行节点选择。因为选择是基于l维空间，因此在新图上的连接性与节点间是一致的。给定一个节点i以及它的特征向量x_i，x_i在p上的标量投影为：

y_i衡量了节点i在投影到p的方向时，有多少信息可以被保留。

假设在图G中有N个节点，每一个节点具有C个特征。这个图可以被表示为两个矩阵；邻接矩阵A^l ∈R^{N×C}，特征矩阵 X^l ∈R^{N×C} 。邻接矩阵中每一个非0项表示图中两个节点的一个边。特征矩阵X^l 的每一行向量x^l_i表示图中第i个节点的特征向量。图池化层l的分层传播规则为：

其中：

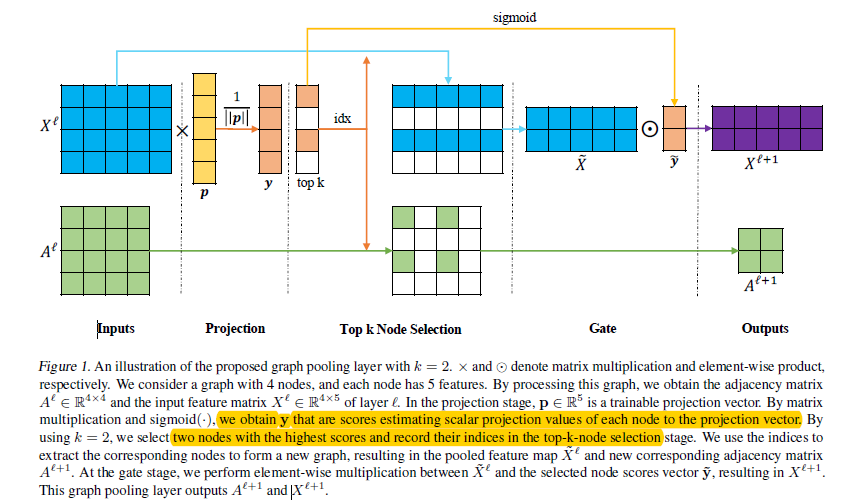
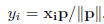
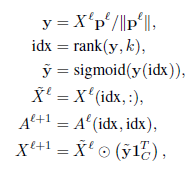
k是新图中被选择的节点数量
rank(y; k)是节点排名操作，返回y中排名靠前的k个值对应的索引
idx是在新图中被选择节点的索引
X^l_{idx,:}是在特征矩阵中通过idx逐行索引
A^l_{idx,idx}是在特征矩阵中通过idx逐行、逐列索引
y(idx)提取y中对应索引的值
1_C∈R^C是由1组成的大小为C的向量

值得注意的是，门操作（上图中的Gate部分）使投影矢量p可以通过反向传播进行训练。

利用幂（power）图增强图的连通性

在上文提出的gPool层，我们对一些重要节点进行采样，以形成用于高级特征编码的新图表。由于在gPool中删除节点时相关的边被删除，因此，在被聚合图中的节点可能被孤立。这可能会影响后续层中的信息传播，特别是当GCN层用于从相邻节点聚合信息时，需要增加被聚合图中的连通性。

为了解决这个问题，我们推出使用图的k阶幂（power）图G^k 去增加图的连接性。这个操作在距离小于等于k跳的节点间建立连接（将G中所有的距离小于等于k的点对连接，获得的新图成为G的k阶幂图，记为G^k）。由于在每个gPool层之前有一个GCN层来聚合来自其一阶相邻节点的信息。因此，在本工作中，我们利用k=2，将上式中的A^{l+1}替换为：

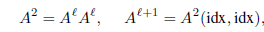
Graph Unpooling 层（上采样）

上采样操作在U-Net等编码-解码网络中是重要的，网络的编码通常使用池化操作以减少特征图的大小并且增加感受野。在解码中，特征图需要被上采样去恢复原始结构。在图像数据中上采样操作有反卷积、以及上采样层。然而，这些操作不能直接在图数据中灵活应用。

为了能够在图数据中使用上采样，我们提出图上采样层（gUnpool)），是图池化层的反操作，将图恢复到最初的结构。

为了能达到这个目的，我们记录在相关图池化层中选择节点的位置，并且使用这些信息去将节点重新放置到图中的原始位置，图上采样层的传播规则如下：

其中：

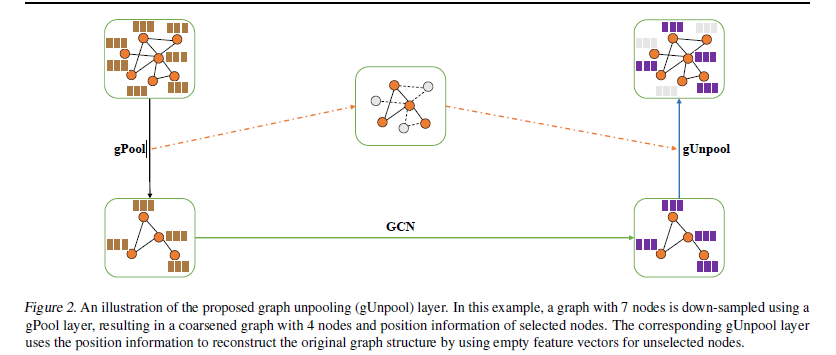
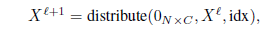
idx∈Z^{*k}包含相应gPool层（将图形大小从N个节点减少到k个节点）中选定节点的索引。
Xl∈R{N×C}是当前图的特征矩阵
0_{N×C}是新图的初始空特征矩阵

distribute()是根据idx中存储的对应索引将X^l中的行向量分配到给初始空特征矩阵0_{N×C}的操作。在X^{l+1} 中，索引为idx的行向量由X^l中的行向量更新，而其他行向量保持为零。

U-Nets框架

在图像数据中，U-Net等解码-编码网络可以在保存本地空间信息的同时对高级特征进行编码和解码。与像素级任务相似，节点分类任务致力于对于每一个输入单元进行预测。基于我们提出的gPool与gUnpool层，我们提出了用于节点分类任务的图U-Nets (g-U-Nets)框架。

在我们的图U-Nets (g-U-Nets)中，由于一些数据集原始的输入通常有一个很高维度的特征向量，我们首先应用一个图嵌入层去将节点转换为低维表示。在图嵌入层之后，我们通过堆叠一些编码块去建立编码器，其中每一个都包含一个gPool层与一个GCN层（GCN层在gPool层之后）。 gPool层减少图的大小去编码高阶特征，而GCN层负责聚集来自每个节点的一阶信息。在解码器部分，我们堆叠解码块，每一个解码块由一个gUnpool层与GCN层组成。 gUnpool层将图形恢复到更高分辨率的结构中，GCN从它的邻居中聚合信息。在编码层与解码层之间有skip-connection，将空间信息传递到解码器以得到更好地表现。 skip-connection可以是特征映射的加和也可以是拼接（concatenation）。最后，在Softmax函数之前使用GCN层进行最终预测。

GCN层的改进

常用的GCN层在归一化之前的邻接矩阵被计算为 ~A=A+I，将自循环添加到图中的每个节点。当执行信息聚合时，向节点自身的特征向量及其相邻节点赋予相同的权重。

在本文中，我们希望对于节点自身的特征向量给予更高的权重，因为它本身的特征对于预测应该更重要。基于此，我们将邻接矩阵的计算改变为~A=A+2I，以此来对图中的自循环施加更大的权重。（文中所有实验均使用此修改版本的GCN层）

实验

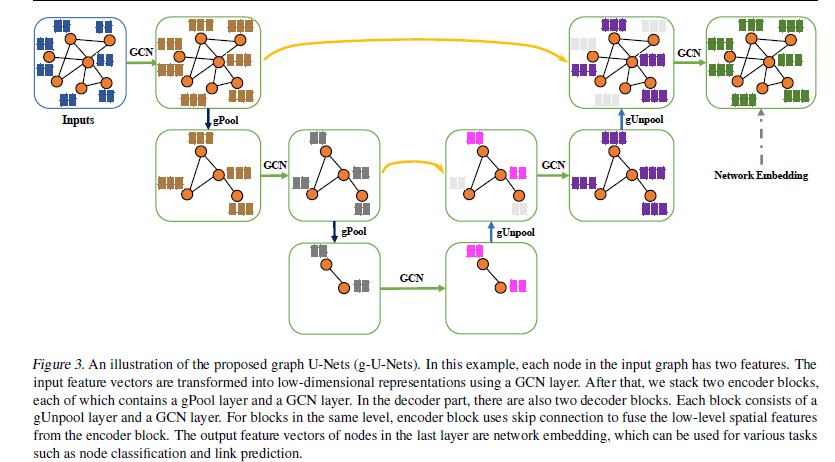
我们主要进行如下三类实验：

将文中中提出的g-U-Nets与节点分类和图分类任务的最新模型进行比较。
进行了一些消融研究，以对比gPool层、gUnpool层和图形连接增强对性能改进的贡献。
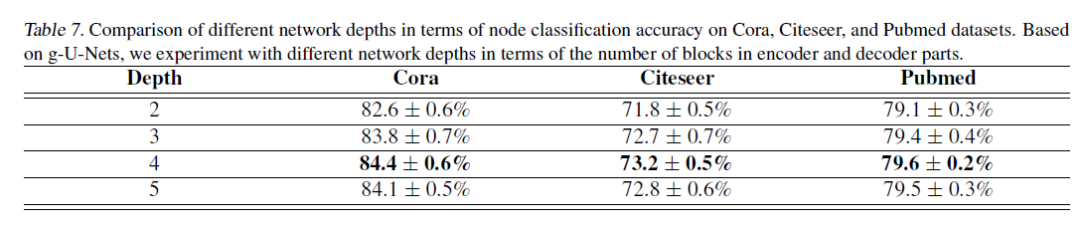
对网络深度与节点分类性能之间的关系进行研究。

数据集

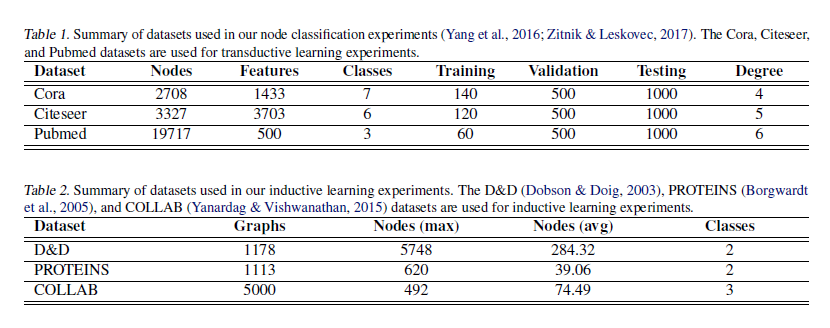
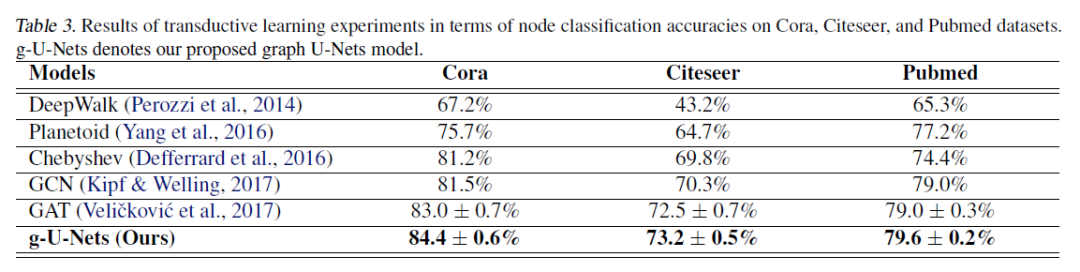
在实验中，我们评估了在转导学习（transductive learning）设置下的节点分类任务和归纳学习（inductive learning ）设置下的图分类任务的网络。

转导学习（transductive learning）设置下，选择Cora，Citeseer和Pubmed（Kipf＆Welling，2017年），总结在表1中。数据集是引文网络，每个节点和每个边分别代表文档和引文。每个节点的特征向量是词袋表示，其大小由字典大小决定。有20个用于训练的节点，500个用于验证的节点和1000个用于测试的节点。
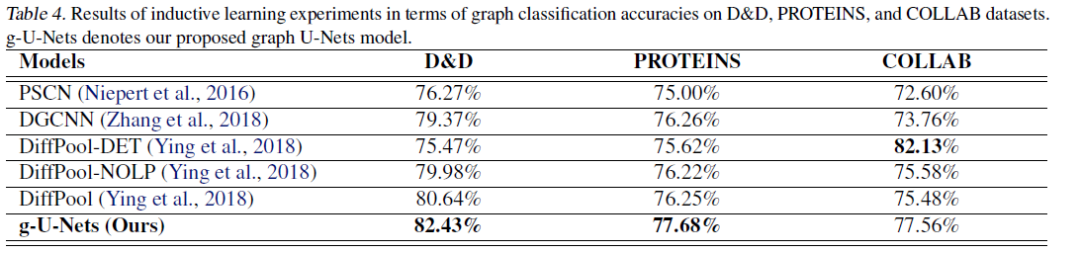
在归纳学习设置（inductive learning ），使用蛋白质数据集D＆D、PROTEINS，科学合作数据集COLLAB。这些数据总结在表2中。