NIPS2018四篇最佳论文出炉,陈天琦、华为公司等获奖
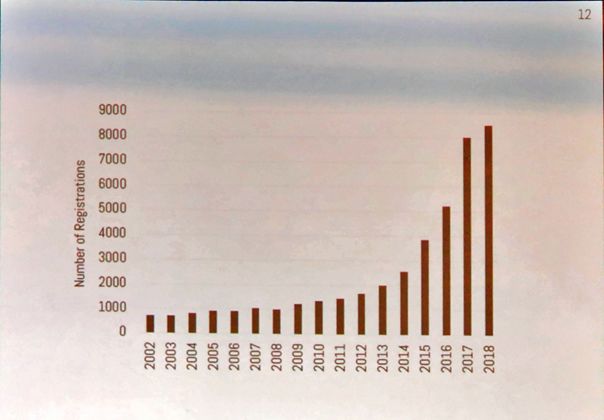
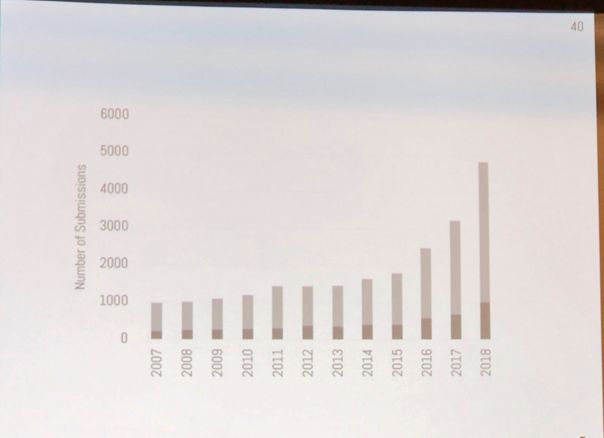
【导读】人工智能领域顶会 NeurIPS 2018 于当地时间 12 月 2 日-8 日在加拿大蒙特利尔举行,2016 年有 5000 人注册参加该会议,2017 年参会人数飙升至 8000,今天参会人数再创新高达到了8400人。 大会总共有4800篇论文提交,录用率21%。
先感受下会场规模
参会人数
投稿人数
录用率
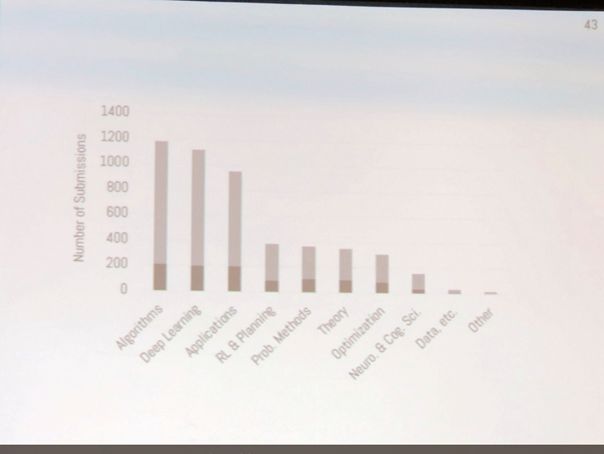
下图是不同领域的投稿录用情况, 可见算法关注度超越深度学习, 之后依次是:应用,强化学习,概率方法,理论,优化方法,神经和认知科学,数据科学等等
同时大会公布了四篇最佳论文
Neural Ordinary Differential Equations
Optimal Algorithms for Non-Smooth Distributed Optimization in Networks
Non-delusional Q-learning and value iteration
Nearly tight sample complexity bounds for learning mixtures of Gaussians via sample compression schemes
Neural Ordinary Differential Equations
作者:Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud。Ricky Tian-qi Chen来自多伦多大学, 跟另外一个XGBoost开发者华盛顿大学计算机系博士生陈天奇重名。
论文地址:
http://www.zhuanzhi.ai/paper/077735925dd83b68f0539b724878603c
http://www.cs.toronto.edu/~rtqichen/
摘要:论文提出了一种新的深度神经网络模型家族,并没有规定一个离散的隐藏层序列,而是使用神经网络将隐藏状态的导数参数化。然后使用黑箱微分方程求解器计算该网络的输出。这些连续深度模型的内存成本是固定的,它们根据输入调整评估策略,并显式地用数值精度来换取运算速度。论文展示了连续深度残差网络和连续时间隐变量模型的特性。此外,还构建了连续的归一化流,一个可以使用最大似然方法训练的生成模型,无需对数据维度进行分割或排序。至于训练,论文展示了如何基于任意 ODE 求解器进行可扩展的反向传播,无需访问 ODE 求解器的内部操作。这使得在较大模型内也可以实现 ODE 的端到端训练。
Optimal Algorithms for Non-Smooth Distributed Optimization in Networks
作者:Kevin Scaman、Francis Bach、Sébastien Bubeck、Yin Tat Lee、Laurent Mas-soulié。作者来自自华为诺亚方舟实验室、INRIA、微软研究院、华盛顿大学等机构
论文地址:
http://www.zhuanzhi.ai/paper/faba4ec5a5f5a67c65e71e659d10642a
摘要:在这行工作中,我们利用计算单元网络,研究了非光滑凸函数的分布优化问题。我们在两个正则性假设下研究这个问题:(1)全局目标函数的Lipschitz连续性,(2)局部单个函数的Lipschitz连续性。在局部正则性假设下,我们提出第一个最优一阶分散算法——多步原对偶算法(MSPD),并给出了相应的最优收敛速度。值得注意是,对于非光滑函数,虽然误差的主导项在中,但是通信网络的结构只影响的二阶项,其中 t 为时间。也就是说,即使在非强凸目标函数的情况下,由于通信资源的限制而产生的误差也会快速减小。在全局正则性假设下,我们提出了一种基于目标函数局部平滑的简单而有效的分布式随机平滑算法(distributed smooth, DRS),并证明了DRS在最优收敛率的乘因子范围内,其中d为底层维数。
Non-delusional Q-learning and value iteration
作者:Tyler Lu、Dale Schuurmans、Craig Boutilier,全都来自Google AI。
摘要:在Q-learning和其它形式的动态规划中,我们确定了一个基本的误差来源。当近似体系结构限制了可表达的贪婪策略类时,就会产生偏差。由于标准Q-updates对可表达的策略类做出了全局不协调的动作选择,因此可能导致不一致甚至冲突的Q值估计,从而导致病态行为,如过高/过低估计、不稳定甚至分歧。为了解决这个问题,我们引入了新的策略一致性概念,并定义了一个本地备份流程,该流程通过使用信息集来确保全局一致性,这些信息集记录了与备份后的Q值一致的策略约束。我们证明使用此备份的基于模型和无模型的算法都可消除妄想(delusional)偏差,从而产生第一种已知算法,可在一般条件下保证最佳结果。此外,这些算法仅需要多项式的一些信息集即可。最后,我们建议尝试减少妄想偏差的Value-iteration和 Q-learning的其它实用启发式方法。
Nearly tight sample complexity bounds for learning mixtures of Gaussians via sample compression schemes
作者:Hassan Ashtiani、Shai Ben-David、Nicholas Harvey、Christopher Liaw、Abbas Mehrabian、Yaniv Plan。
论文地址:
http://www.zhuanzhi.ai/paper/faba4ec5a5f5a67c65e71e659d10642a
摘要:我们证明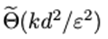
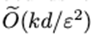
时间检验奖论文
一篇时间检验奖论文授予了2007年发表的论文:The Tradeoffs of Large Scale Learning
作者:Leon Bottou、Olivier Bousquet,分别来自NEC美国实验室和Google。
在这篇论文中,作者考虑到实例数量和计算时间的预算约束,发现了小规模学习系统和大规模学习系统的泛化性能之间存在质的差异。作者指出,大规模学习系统的泛化属性,取决于估计过程的统计特性和优化算法的计算特性。
-END-
专 · 知
人工智能领域26个主题知识资料全集获取与加入专知人工智能服务群: 欢迎微信扫一扫加入专知人工智能知识星球群,获取专业知识教程视频资料和与专家交流咨询!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请加专知小助手微信(扫一扫如下二维码添加),加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
请关注专知公众号,获取人工智能的专业知识!
点击“阅读原文”,使用专知