从最大似然估计思维（参数估计）到深度学习

在这个深度学习盛行的年代，想沉下心来了解一些基础而不是每日调包调参比较难，抽个空特此写下比较全面的笔记。

贝叶斯学派与频率学派的区别

这俩学派的区别很隐晦，看过很多文章都一知半解缺乏直观认识，这里我举个例子来阐述自己的理解吧。假设投掷一枚不规则的硬币（但还是只有上下两面）, 在已知观测数据x 上，想要知道硬币朝上的概率 \theta 。

• 贝叶斯方法会将 \theta 看做未知的随机变量，且它具备某种先验分布，利用后验概率分布推导 x 情况下， \theta 发生的概率 p(\theta|x) ，目的是得到同时包含先验知识和观测值所能提供的关于 \theta 的信息。
• 经典统计方法会将 \theta 看做是一个常数，从哲学角度讲就像飞机的原理，不管发现与没发现它，它从宇宙大爆炸开始就一直存在着，只是它是未知的。所以我们需要去估计它，且尽量地逼近这个未知，往往需要海量的测试，最终目的是得到 \theta 的估计方法并满足该方法必须具备的性质。

因此，在极大的数据样本情况下，两个学派殊途同归。

极大似然估计

一个典型的频率派方法，我会以从简到难的思路来阐述它。

a、还是投硬币的例子，一个均匀的硬币朝上的概率是 \frac{1}{2} ，想计算“投掷5次，有2次朝上”的这个情况发生的概率为多少？

C_{5}^{2} \cdot \left( \frac{1}{2} \right)^{3}\cdot \left( \frac{1}{2} \right)^{2} = \frac{5}{16} \approx 0.312\\

b、复杂一点，假设有两个不均匀的硬币，你通过某种途径知道了第一枚硬币朝上的概率为 \frac{3}{5} ，第二枚硬币朝上的概率为 \frac{2}{5} , 想知道“投掷5次，有2次朝上”这个情况发生谁的概率最高？

硬币1： C_{5}^{2} \cdot \left( \frac{3}{5} \right)^{2}\cdot \left( \frac{2}{5} \right)^{3} \approx 0.230\\

硬币2： C_{5}^{2} \cdot \left( \frac{2}{5} \right)^{2}\cdot \left( \frac{3}{5} \right)^{3} \approx 0.345\\

所以我们想获取 “投掷5次，有2次朝上”这样一个模型，最好的情况是拿第二枚硬币。

c、再复杂一点，一枚不均匀硬币朝上的概率是未知的, 但我们做了海量的实验，投了5次，有2次正面，设正面的概率为 p ，则似然函数为：

L= (1-p)^4\cdot p^6 \\

那这个式子的理解需要结合前面的例子，是在硬币朝上的概率为 p 的情况下,“投5次，2次正面朝上”这个事情(A)发生的概率是多少，而我们实验观测到这事情已经发生，要寻找这个未知的 p ,使得A发生的概率尽可能大。求极值的方法这里简述：求导令其为0，而直接求导有些麻烦（有指数的求导），两边对数化（单调性不变）得到：

ln(L)=3\cdot ln(1-p)+2\cdot ln(p) \\

求导并让其＝0：

-\frac{3}{1-p} + \frac{2}{p} = 0 \\

显然 p=\frac{2}{5} , 和上一种情况吻合了,这一枚硬币属于b、的第二枚硬币那一类，可类比深度学习中的猫与狗的分类，嗯，又一个“飞机的原理”被找到了。

这大概就是参数估计的思路了，似然性 L(p|A) 从观测结果 A 出发，分布函数的参数为 p 的的可能性大小，而b、则是在参数 p 已知的情况下，发生观测结果A的概率 P(A|p) 。而现实中我们们追求未知，往往追求的就是这个 p 。

为了更清晰地认识这个原理，再换个角度去理解以上内容，似然函数如下：

L(p|A) = P(A|p)\\

其中A已知（即“投5次，2次正面朝上），未知的是朝上的概率 p , 对于两个参数结果， p_1 = \frac{2}{5}, p_2=\frac{3}{5} , L(p_1|A) = P(A|p_1) > L(p_2|A) = P(A|p_2) ，意味着若观测数据为A， p = p_1 比 p = p_2 更有可能成为这个分布函数的参数。

d、继续复杂一点，我们获取了N张图片，只有猫和狗两种类型，而我们想拟合一个函数：

y = w^Tx+b \\

这个函数能尽可能地让我们去判断，除N张图片以外，其它图片是猫还是狗。所以我们会得到一个关于图片特征 x 的线性函数并且向让输出 y 尽可能地使得“该张图为猫”（or 狗）这个事情的几率靠近1，这语法结构很容易让人联想到似然性的描述。但是这样的话 y 应该在0,1之间，而输出值很有可能比1大或者为负值，所以我们需要sigmoid函数让线性函数转换为非线性函数。为什么用它，可以参考我的另一篇笔记，嫌弃写得不好也可以在别处找找。

还是从简到难的思路吧吧。

举个例子：下面这批数据为大小为 3×3 的灰度图， x\subseteq R^{3\times3}

我们希望得到一组参数 w 、 b 去拟合函数并分类图像，也就是做出一个分类器，以图片特征向量为输入，预测输出结果 Y 是 1 还是 0 来确定图片中是猫还是狗。我们把图片压缩成一个向量 x=(n_x,1) , 以 Y 表示输出结果， (x^i,Y^i) 表示第 i 组训练数据， X = [x^1,x^2,...,x^m] 表示所有训练数据集的输入值，放在一个 n_x\times m 的矩阵中。

简化就是 x=(9,1) , X = [x^1,x^2,x^3,x^4] ,所有数据放在 9\times 4 的矩阵中。

\tilde{y}^i= \sigma(w^Tx^i+b), where: \sigma(z) = \frac{1}{1+e^{-z}}\\ Given:{ (x^1,y^1), (x^2,y^2), (x^3,y^3), (x^4,y^4) } \\ Want:{\tilde{y}^i \approx y^i}

我们需要损失函数又叫做误差函数，来衡量算法的运行情况，Loss function: L（\tilde{y},y）,通过这个损失函数来衡量预测值与实际值有多接近，因为我们想让 \tilde{y} 尽可能地靠近 y ，但我们一般不用最小二乘法来评价，原因梯度下降法可能找不到全局最优值，即陷入局部最优值（左）。

而我们需要的右边那样的损失函数曲线（凸函数）。

以最大似然思想为基础，目标是要最大化似然概率： max \prod_{i=1}^{4} p(y^i|x^i,\theta) （1）

对于二分类问题有: p = p(y|x,\theta) = p_{1}^{y^i} \times p_{0}^{1-y_i}\\ where: p _1 denotes 猫，p_0denotes 狗

带入（1）得： max \sum_{i=1}^{4}{y^ilog(p_1)+(1-y^i)log(1-p_1)}

将max改为min(加负号)获得最终损失函数形式：min-\frac{1}{4}\sum_{i=1}^{4}{y^ilog(\tilde{y}^i)+(1-y^i)log(1-\tilde{y^i})}

要让 L(\tilde{y},y) 尽可能小，跳跃到之前的似然函数处理方式，也就是求导了。而在神经网络中，则是梯度下降法，如下图所示：

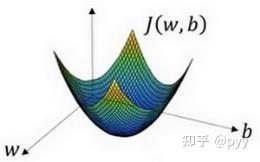
我们会初始化 w,b，是其落在上图的某个点

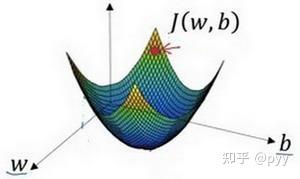
梯度下降法就是朝着最小值点方向走

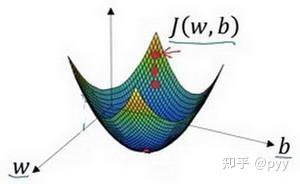
不断地更新w和b， w:=w-\alpha\frac{\partial{J(w,b)}}{\partial{w}}\\ b:=b-\alpha\frac{\partial{J(w,b)}}{\partial{b}}\\

而alpha表示学习率，想象一下如果学习率过大会有什么问题？过小呢？

深度学习

还是从简到难，由浅入深，结合之前的九维猫狗特征输入值，我们搞个简单的三层神经网络。

每个圆圈表示一个包含激活函数的神经元，[1] 表示第一层，默认输入层为第0层，下标1表示第一个神经元，所以这里第一层的w参数是9×9大小的矩阵，b是9×1的向量，第二层输出层的w参数是1×9向量，b是1×1向量，a表示每个神经元的输出。

这里的计算公式为： z = w^T+b \Rightarrow a = \sigma(z) \Rightarrow L(a,y) , 这里损失函数的处理方式之前已经说过。然后利用导数的链式法则，反向传播更新参数w,b，至于反向传播过程这里不赘述了。

最后我们能保存的模型就是这一堆 w,b 的参数，从而计算出一个图片在哪一类。而深度神经网络就是加神经元，加网络层数。

以上纯属笔记，有错误望大佬指出。