什么是无监督学习？

本课程来自清华大学计算机系唐杰老师。

授课教师主页： http://keg.cs.tsinghua.edu.cn/jietang/

课程主页：https://www.aminer.cn/aml

1 本节目录

• 聚类
• K-means, K-medoids, 层次聚类
• 混合模型

• 降维
• 主成分分析 PCA
• 谱聚类

2 聚类

• 聚类意为将数据中相似的样本分为一类，数据本身并不含标签信息。
  
• 聚类原则(判别聚类质量)为，类内距离小(高相似度)，类间距离大(低相似度)。
  

2.1 聚类的类别

• 聚类可分为划分聚类(Partitional Clustering)，层次聚类(Hierarchical clustering)
  
• 划分聚类为直接将数据分割成不重叠的子集(自顶向下)；
  
• 层次聚类为先讲局部相似的数据划分为较低级别的小类，再依据小类进行大类别的聚类(自底向上)
  
• 图示对比
  

数据为\boldsymbol x_i=[x_{i1},x_{i2},\dots,x_{im}]

数据矩阵为

\left[\begin{aligned}x_{11}\quad &\cdots\quad x_{1k} \quad \cdots\quad x_{1m}\\\cdots\quad & \cdots\quad \cdots\quad \cdots\quad \cdots\\x_{i1}\quad &\cdots \quad x_{ik} \quad \cdots \quad x_{im}\\\cdots\quad & \cdots\quad \cdots\quad \cdots\quad \cdots \\x_{N1}\quad &\cdots\quad x_{Nk} \quad \cdots \quad x_{Nm} \end{aligned}\right] \\

2.2 划分聚类

• 基本概念：将数据集D中的N个样本分到k个类别中。
• 给定k，优化选择好的划分指标
• 全局最优；穷举所有划分方式
• 启发式方法：k-means 与k-medoids
• k-means 每个类由聚类中心代表
• k-medoids PAM (Partition around medoids)每个类由每个类别中的一个数据点代表

2.2.1 k-means

• k-means算法有四个步骤
  
• 给定聚类类别数k；
• 计算每个类别的聚类中心，例如取数据的平均值为聚类中心；
• 将数据分配到距离其最近的聚类中心所属类别；
• 重复第二步，直到没有新的分配。

• k-means算法图示

• 相似度度量
  
• 距离函数：d(i,j)
  
• 闵可夫斯基距离
  d(i,j)=\sqrt[q]{(|x_{i1}-x_{j1}|^q+|x_{i2}-x_{j2}|^q+\dots+|x_{ip}-x_{jp}|^q)}
  q=1时为曼哈顿距离，q=2时为欧几里得距离
  
• 余弦相似度
  \frac{x^Ty}{|x||y|}
  

• k-means优缺点
• 优点：相对高效：\mathcal{O}(tkn). n为样本数，k为聚类类别数，t为迭代次数。通常k,t\ll n
  
• 对比其他算法复杂度：PAM : \mathcal{O}(k(n-k)^2)，\mathcal{O}(ks^2+k(n-k))
• 缺点：
  
• 要求类别样本的平均值有定义，如果是对类别数据进行聚类呢？
• 需要指定k；
• 无法处理带造数据与离群点；
• 不适合发现非凸的聚类类别。
• 可能找到的是局部最优解，全局最优解可能需要借助启发式算法，例如退火算法或者遗传算法。
• 初始聚类中心的选取
  
• 多次选择，多次运行算法
• 采样与层次聚类结合进行初始化
• 选择多于k个聚类中心点，选择最散开的点作为聚类中心
• 后处理
• k-means的两个可能不符合预期的聚类结果图示，由数据疏密程度引起的或者数据包含结构化的信息。
  

2.2.2 k-medoids

• k-means对于离群点敏感，可能破坏数据分布信息。
• k-medoids与k-means的区别是选择数据点作为聚类中心。

• k-medoids算法流程

代表性的方法

• PAM (Partitioning Around Medoids, 1987)

使用贪婪搜索，可能无法找到最优解，但是运行比穷举搜索快；

初始化：贪婪地选择具有最小化损失的k个聚类中心点；

将每个数据点与最近的聚类中心联系起来；

重复以下步骤：

​ 在更新聚类中心点i时，计算每个非聚类中心点h与聚类中心交换时总的损失TC_{ih}

​ 找到一个数据对(i,h)能够最小化损失TC_{ih}

​ 如果损失TC_{ih}{<}0，则更新聚类中心

直到\min TC_{ih}>0

​ 计算复杂度：

​ 每次迭代\mathcal{O}({k(n-k)^2})，交换i,h，TC_{ih}=\sum_jC_{jih}

• CLARA (Kaufmann & Rousseeuw, 1990)
  Clustering LARge Applications 基于采样方法，每次从数据集中采样出组个样本，应用PAM聚类
  优点：可以在大规模数据上应用
  缺点：效率取决于每组样本的数据量s, \mathcal{O}(ks^2+k(n-k))
  ​ 如果采样是有偏差的，那么此方法给出的结果并不好。
  
• CLARANS (Ng & Han, 1994)
  只在一些可能会有交换的子集上计算，复杂度\mathcal{O}(n^2)
  
• Focusing + spatial data structure (Ester et al., 1995)
  

• 层次聚类依据近似度矩阵进行自底向上的聚类

• 衡量类间相似度的方法
  
• 最小值
• 最大值
• 类平均值
• 类别中心的距离
• 其他目标函数为导向的方法
• Ward的方法使用平方误差

• 层次聚类复杂度
  
• 空间复杂度：\mathcal{O}(N^2)，因为使用了近似度矩阵(N为数据样本点个数)。
• 时间复杂度：\mathcal{O}(N^3)，N步每步都要更新近似度矩阵。
• 时间复杂度能够降为\mathcal{O}(N^2\log(N))。
• 层次聚类的限制：
  
• 高层次的聚类是依赖低层次的聚类的，高层聚类无法对底层聚类做出反馈以改善结果；
• 没有直接优化的目标函数；
• 其他存在的问题：对噪声数据与离群点敏感；难以处理不同尺度类别；破坏了大型聚类类别。

2.4 混合模型

• k-means的问题
  
• 硬指派(分类)：数据点被确定为唯一的类别
  
• 实际中聚类类别可能是有重叠的
  

• 混合模型使用K个具有不同分布参数的同类分布(例如高斯分布)共同拟合数据分布规律。
• 隐变量：指定每个观测点属于哪个分布，用z_i来表示。
• 混合权重：
• 概率合为1
• \phi_i第i个先验概率分布
• z_i\sim\text{Multinomial}(\phi)

2.4.1 高斯混合模型 GMM

• 混合分布为几个多元高斯分布的凸组合
  p(x)=\sum_kp(k)p(x|k)=\sum_k\phi_k\mathcal{N}(x|\mu_k,\Sigma_k)

• 在高斯混合模型中，数据被认为是这样构成：先确定数据服从哪个高斯分布，然后再从该高斯分布中进行采样。
  
• GMM模型参数\phi,\mu,\Sigma
  
• GMM模型似然函数：
  
• \mathcal{L}(\phi,\mu,\sigma)=\sum_ip(x_i;\phi,\mu,\sigma)=\sum_i\log\sum_jp(x_i;\mu,\Sigma)p(z_i;\phi)
• 似然函数对模型参数求导，会发现此处没有闭式解，在经典算法中解GMM使用期望最大化EM算法。

• 期望最大化算法：
  
• EM算法用来求解似然函数中包含观测不到的隐变量时的情形，分为以下两步
• E步：给定当前参数估计；输出z_{ij}；给定Q(\theta|\theta^{(t)})：给定当前估计时log似然的期望；
• M步：最大化函数Q
• 在GMM中，函数Q为

• EM算法解GMM步骤描述

• EM算法与k-means的关系
• E步：聚类
• M步：更新聚类中心

3 降维

• 降维即降低数据的维度，找到数据中的主要成分变量。
  
• 数据集为X\in R^{N\times m },希望得到\tilde X\in R^{N\times K},K\ll m
  
• 应用：数据可视化，数据压缩
  

3.1 主成分分析PCA

• 在降维时，要保留尽可能多的信息，最小化表示原始数据的平方误差。例如下图，比起方向u_2来说，更应该把数据投影到u_1方向上。在这个方向上更能体现数据原始分布特征。

• 主成分分析使用蒸饺线性变换进行降维。
  
• \tilde x_n=x_n^T u_1,\|u_1\|_2=1，例如下图，将红色点与主成分方向做内积，将数据投影到紫色线上，投影结果为绿色点。

• 主成分方向：以最大方差方向作为第一主成分，第二大方差方向作为第二主成分...
  
• 找到第一主成：最大化方差
  
• \max \frac{1}{2N}\sum_n(u_1^Tx_n-u_1^T\bar{x})^2=\max u_1^TSu_1,\|u_1\|=1
• 上式中\bar x为原始数据平均值，S为原始数据方差
• 瑞利商：R(S,u_1)=\frac{u_1^TSu_1}{u_1^Tu_1}\leq\lambda_{max}，可知u_1为方差矩阵最大特征值对应特征向量方向。

• 类似的，寻找第二主成分，结果为方差矩第二大特征值对应特征向量方向，所以可求出方差矩阵的前K个特征向量。实际中使用奇异值分解完成特征方向的计算。
  
• 以上讲的主成分方向标准是最大化投影后数据的方差，它与最小化投影结果到原始数据的重构误差是等价的，如下图。
  

• K取多大？在实际中可检查有多少数据方差被表示出来了，当取的成分数，保留了80\%-90\%的方差时，可认为所取K是合理的。
• PCA缺陷，当数据维度较高时，协方差矩阵太大了，难以进行奇异值分解。

知识补充

• 奇异值分解(singular value decomposition, SVD)：定义：对于矩阵X\in R^{n\times m}存在如下分解形式
  X=UDV^T,这些矩阵尺寸分别为U [n\times r], D[r\times k], V[m\times k]
  奇异值分解的几何意义：矩阵变换M，可视为先对原几何图形进行旋转(V)，对不同方向进行缩放(\Sigma)，再次旋转(U)
  

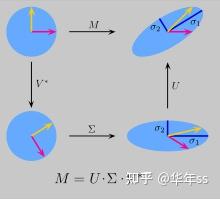
• U被称为左奇异向量，是XX^T的特征向量
  
• V被称为右奇异向量，是X^TX的特征向量
  
• 矩阵X的非零奇异值为X^TX特征值的平方根
  
• SVD的一个有用特性是推广了非方形矩阵的逆。

• 截断SVD
  TSVD仅考虑几个奇异值成分，将矩阵分解为如下形式。复杂度为\mathcal{\min(m^2n,mn^2)}

• 快速随机tSVD算法简要叙述
  
• A步：构建低维子空间近似X的列构成的空间。X\approx QQ^TX,Q [m\times k,k\ll\min(m,n)]
  Y=A\Omega，\Omega是高斯随机值
  Y=QR
  
• B步：B=Q^TX，进行tSVD B=SDV^T,QS=U
  
• 结果X=QB。此分解方法可显著加速奇异值分解速度

4 谱聚类

• 课程将这一聚类模型放在了最后进行讲解。
• 谱聚类，将数据构造为无向图，通过对图的分割进行聚类。

4.1 切割无向图

• 图由节点与边组成G(V,E)，依据最大化类内连接(高内聚)，最小化类间连接(低耦合)，对图进行分割。

• 将聚类目标函数表述为切分边的代价(类似于目标是以最低的能量损耗将大分子分为小分子)
  cut(A,B)=\sum\limits_{i\in A,j\in B}w_{ij}
  w定义为节点之间的边，如果有连接是1，没有连接是0。那么下图切分cut(A,B)=2

• 切分准则：最小化切割
  \arg \min_{A,B}=cut(A,B)
  使用如上目标函数的缺陷，没有考虑类内结构化信息。
  

• 对于这个准则的一些改进是，使用某类的节点数或所有边的和进行归一化
  RatioCut(A,B)=cut(A,B)/|A|
  NCut(A,B)=cut(A,B)/\min(vol(A),vol(B))
  

知识补充

• 以上文所述节点之间的边为元素构成的矩阵称为邻接矩阵A(Adjacency matrix)
  
• 节点数为n，则A的大小为n\times n
• A中的元素A=[a_{ij}]，为节点i,j之间的边
• A为人为定义值，例如可将边定义为如果两个节点之间有连接，则a_{ij}=1，否则为a_{ij}=0
• 重要性质：
• 邻接矩阵是对称矩阵
• 具有n个实特征值
• 特征向量是实值，且凉凉正交的

• 举例：简单的邻接矩阵

• 
  度矩阵(Degree matrix)
  
• 定义：D=\text{diag}(\sum_iA_{ij})对角矩阵
• 如果邻接矩阵为上述所说的简单情况，那么度矩阵含义为当前节点的邻居数目，如下图所示。

• 拉普拉斯矩阵(Laplacian matrix)
  
• 定义：L=D-A，根据邻接矩阵的性质可知，L也是实对称矩阵

• 如果邻接矩阵为上述所说的简单情况，那么假设有一向量为全一向量x=(1,\dots,1)，则Lx=0，可知0为L的最小特征值。
  
• 拉普拉斯矩阵的特殊性质
  
• 所有特征值大于等于0
  
• 任取x，有x^TLx=\sum_{ij}L_{ij}x_ix_j\geq0
  
• L可被拆分为L=N^TN
  
• 以上都是实对称矩阵的性质
  
• 有如下重要关系
  f^TLf=\frac{1}{2}\sum_{ij}w_{ij}(f_i-f_j)^2
  

4.2 RatioCut

• 回顾以上RatioCut损失函数RatioCut(A,B)=cut(A,B)/|A|。下面叙述如何将这一聚类转化为优化问题。
  
• 现对于每个聚类的类别都引入一n维指示向量h_j=\{h_1,\dots,h_k\}，定义如下
  
• 对于类A_j，如果第i个节点属于当前类，则h_{ji}=\frac{1}{\sqrt{|A_j|}}，否则h_{ji}=0
  
• 并且有如下关系(不知道怎么想到的)
  

• 当考虑多个类别聚类时，总的损失函数为。并且H^TH=I

• 则此时损失函数又变为了与上文所述主成分分析类似的瑞利商的形式。虽然H被定义为离散值，但此时其已经被放缩到连续值上。
  
• 聚类最终依据：依据瑞利商的性质，当聚类k个类别时，H的解为L最小的k个特征值对应的特征向量。则可根据特征向量的数值分布情况，对特征向量组成的矩阵进行k-means聚类，达到对原始图聚类的目的。依照上文所述，L的最小特征值为0，则依据这个特征值对应的特征向量无法判定聚类结果，本课程中讲述的方法是使用L第二小特征值对应的特征向量进行判定，特征值、特征向量与聚类图示如下图
  
  

• 更多RatioCut结果图示

• 如何选择类别数k
  
• 一般选择使得下式最大化的k
  \Delta _k=|\lambda_k-\lambda_{k-1}|

5 无监督学习未来方向

• 预训练

• 自监督学习

推荐阅读