知识图谱的低维双曲嵌入

本次介绍的论文《Low-Dimensional Hyperbolic Knowledge Graph Embeddings》来自斯坦福大学Christopher组，目的是研究知识图谱在双曲空间下对多关系表示的研究。

Abstract

知识图谱具有层次性与逻辑关系（对称、非对称、自反等），双曲空间下的知识图谱表示可学习到知识图谱的层次性，但却无法学习知识图谱中蕴含的丰富逻辑关系。该工作的核心即在双曲空间下同时学习知识图谱的层次性与逻辑关系。

Introduction

知识图谱存在对称、非对称等多类型的关系，对这些关系进行高效建模是一种挑战。现有的双曲知识图谱嵌入方法的结构表达能力非常强，但仍缺乏对多关系类型表示的能力。为了实现层级性与逻辑模式的双重表达，作者进行如下工作：（1）学习特定关系的曲率，不同曲率代表双曲空间“弯曲”的程度不同。（2）参数化双曲等高线，利用其几何特征捕获诸如对称、非对称等逻辑模式。（3）使用“双曲注意力”将几何操作符与捕获多逻辑模式结合起来。

“反射”对应对称关系，“旋转”对应非对称关系。

Related Work

欧式空间下的embedding方法参数数量少、直观简单，但无法表示复杂关系。复数空间下的embedding需要很高维度，造成高内存占用。图神经网络训练的embedding需要预训练，计算代价较大。双曲空间下的知识图谱表示在2019年爱丁堡大学在NIPS上发表过《Multi-relational Poincaré Graph Embeddings》，该工作的MURP模型对知识图谱的层级结构进行建模，但仍然使用基于平移的方法，无法学习复杂的关系模式，且双曲空间的曲率固定，对不同性质的关系并不友好，同时使用了复杂的黎曼优化，增大了训练难度。

Background

该工作使用d维、曲率为-c(c>0)的庞加莱球： B^{d,c} = \left\{ x \in R^{d} : \left| \left| x \right|\right|^{2} < \frac{1}{c} \right\} ，对于 x\in B^{d,c} ，正切空间 \Gamma_{x}^{c} 包含该点在庞加莱球面上所能到达的所有方向。

正切空间到庞加莱球的转换：

exp_{0}^{c}(v) = tanh(\sqrt{c}\left| \left| v\right|\right|)\frac{v}{\sqrt{c}\left|\left| v\right|\right|}

庞加莱球到正切空间的转换：

log_{0}^{c}(y) = arctanh(\sqrt c \left|\left| y \right|\right|) \frac{y}{\sqrt c \left|\left| y \right|\right|}

庞加莱球面上的距离公式：

d^{c}(x,y) = \frac{2}{\sqrt c}(\sqrt c \left|\left| -x \oplus^{c} y \right|\right|)

Methodology

参数化使用 \Theta_{r} := (\theta_{r,i})_{i\in \left\{ 1,...,\frac{d}{2} \right\}} ，\Phi_{r} := (\phi_{r,i})_{i\in \left\{ 1,...,\frac{d}{2} \right\}}

Rot(\Theta_{r}) = diag(G^{+}(\theta_{r,1}),...,G^{+}(\theta_{r,\frac{d}{2}}))

Ref(\Phi_{r}) = diag(G^{-}(\phi_{r,1}),...,G^{-}(\phi_{r,\frac{d}{2}}))

\Rightarrow G^{\mp}(\theta) := \left( \begin{array}{ccc} cos(\theta) & \mp sin(\theta) \\ sin(\theta) & \pm cos(\theta) \\ \end{array} \right)

使用注意力模型表示“即不是对称，也不是非对称”的关系：

假设 x^{H} 与 y^{H} 是双曲空间内的点， \alpha 是attention向量。

先进行双曲-正切空间的转换， x^{E} = log_{0}^{c}(x^{H}) 、 y^{E} = log_{0}^{c}(y^{H}) 。

再进行注意力计算： (\alpha_{x},\alpha_{y}) = Softmax(\alpha^{T}x^{E},\alpha^{T}y^{E})

加权求和： Atth(x^{H},y^{H};a) := exp_{0}^{c}(\alpha_{x}x^{E}+\alpha_{y}y^{E})

ATTH模型：

给定知识图谱中的三元组(h,r,t)，使用Rotation与Reflection参数分别对头实体h进行变换，得到：

q_{Rot}^{H} = Rot(\Theta_{r})e_{h}^{H} ， q_{ref}^{H} = Ref(\Phi_{r})e_{h}^{H}

计算注意力并进行平移变换：

Q(h,r) = Att(q_{Rot}^{H},q_{Ref}^{H};\alpha_{r})\oplus^{c_{r}}r_{r}^{H}

通过打分函数计算：

s(h,r,t) = -d^{c_{r}}(Q(h,r),e_{t}^{H})^{2} + b^{h} + b_{t}

Experiments

dataset

实验用到的数据集

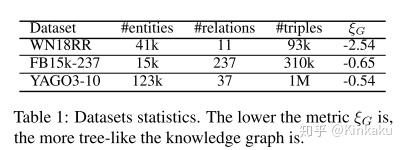
\xi_{G} 越小，代表数据集越像一棵树，即具有更强的层次性特征。

消融实验

将曲率设置为0，即为弯曲程度为0的欧式空间进行对比；将旋转与反射分别替换注意力机制后的结果。

损失函数

L = \prod_{t^{'}\sim U(V)}log(1+exp(y_{t^{'}}s(h,r,t^{'}))) \\ \Rightarrow y_{t}^{'} = \begin{cases} -1 & \text{if } t^{'} = t \\ 1 & otherwise \end{cases}\\