梯度下降入门
本文参考深入浅出--梯度下降法及其实现,对后面将公式转化为矩阵的形式加了些解释,便于大家理解。
梯度下降是用来求函数最小值点的一种方法,所谓梯度在一元函数中是指某一点的斜率,在多元函数中可表示为一个向量,可由偏导求得,此向量的指向是函数值上升最快的方向。公式表示为:
\[\nabla J(\Theta) = \langle \frac{\overrightarrow{\partial J}}{\partial \theta_1}, \frac{\overrightarrow{\partial J}}{\partial \theta_2}, \frac{\overrightarrow{\partial J}}{\partial \theta_3} \rangle
\]
比如
\[\begin{aligned}
J(\theta) &= \theta^2 \qquad \nabla J(\theta) = J'(\theta) = 2\theta\\
J(\theta) &= 2\theta_1+3\theta_2 \quad \nabla J(\theta) = \langle 2,3 \rangle
\end{aligned}
\]
由于梯度是函数值上升最快的方向,那么我们一直沿着梯度的反方向走,就能找到函数的局部最低点。
因此有梯度下降的递推公式:
\[\Theta^1 = \Theta^0 - \alpha \nabla J(\Theta^0)
\]
其中\(\alpha\)称为学习率,直观得讲就是每次沿着梯度反方向移动的距离,学习率过高可能会越过最低点,学习率过低又会使得学习速度偏慢。
为了更好的理解上面的公式
我们举例:
\[\quad J(\theta) = \theta^2 \Longrightarrow \nabla J(\theta) = J'(\theta) = 2\theta
\]
则梯度下降的迭代过程有:
\[\begin{aligned}
\theta^0 &= 1 \\
\theta^1 &= \theta^0 - \alpha \times J'(\theta^0) \\
&= 1-0.1 \times 2 \\
&= 0.2 \\
\theta^2 &= \theta^1 - \alpha \times J'(\theta^1)\\
&= 0.04\\
\theta^3 &= 0.008\\
\theta^4 &= 0.0016\\
\end{aligned}
\]
我们知道$J(\theta) = \theta^2 \(的极小值点在\)(0,0)\(处,而迭代四次后的结果\)(0.0016,0.00000256)$已相当接近。
再举一个二元函数的例子:
\[J(\Theta) = \theta_1^2 + \theta_2^2 \Longrightarrow \nabla J(\Theta) = \langle 2\theta_1 + 2\theta_2 \rangle
\]
令\(\alpha = 0.1\), 以初始点\((1,3)\)用梯度下降法求函数最低点
\[\begin{aligned}
\Theta^0 &= (1,3) \\
\Theta^1 &= \Theta^0 - \alpha \nabla J(\Theta^0)\\
&= (1,3) - 0.1(2,6)\\
&= (0.8,2.4)\\
\Theta^2 &= (0.8,2.4) - 0.1(1.6,4.8)\\
&= (0.64,1.92) \\
\Theta^3 &= (0.512,1.536) \\
\end{aligned}
\]
值得注意的是,迭代的效率除了和步长(学习率)\(\alpha\)有关外,还与初始值的选取有关。
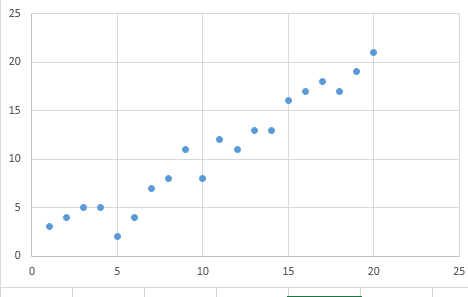
梯度下降做散点拟合
\[\begin{aligned}
&\nabla J(\Theta) = \langle \frac{\delta J}{\delta \theta_0}, \frac{\delta J}{\delta\theta_1} \rangle \\
&\frac{\delta J}{\delta \theta_0} = \frac{1}{m} \sum_{i=1}^m \left\lbrace h_\Theta(x_i) - y_i \right\rbrace\\
&\frac{\delta J}{\delta \theta_1} = \frac{1}{m} \sum_{i=1}^m \left\lbrace h_\Theta(x_i) - y_i \right\rbrace x_i\\
\end{aligned}
\]
为了便于利用python的矩阵运算,我们可以将公式稍微变形
\[\begin{aligned}
h_\Theta(x_i) &= \theta_0 \times 1 + \theta_1 \times x_i \\
&=
\begin{bmatrix}
1 & x_0\\
1 & x_1\\
\vdots & \vdots\\
1 & x_{19}\\
\end{bmatrix}
\times
\begin{bmatrix}
\theta_0\\
\theta_1
\end{bmatrix}
\end{aligned}
\]
\(i\)的范围是\([1,20]\),因此最后得到
\[h_\Theta(x_i)=
\begin{bmatrix}
h_0\\
h_1\\
\vdots\\
h_{19}
\end{bmatrix}
\]
\[误差diff =
\begin{bmatrix}
h_0\\
h_1\\
\vdots\\
h_{19}
\end{bmatrix}-
\begin{bmatrix}
y_0\\
y_1\\
\vdots\\
y_{19}
\end{bmatrix}
\]
\[方差和
\sum_{i=1}^m \left\lbrace h_\Theta(x_i) - y_i \right\rbrace ^2=diff^T \times diff
\]
将公式变为矩阵向量相乘的形式后你应当更容易理解下面的python代码
import numpy as np
# Size of the points dataset.
m = 20
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
def error_function(theta, X, y):
'''Error function J definition.'''
diff = np.dot(X, theta) - y
return (1./(2*m)) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
theta = np.array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, y)
while not np.all(np.absolute(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, y)
return theta
optimal = gradient_descent(X, y, alpha)
print('optimal:', optimal)
print('error function:', error_function(optimal, X, y)[0,0])
转载请保留原文链接及作者
| 本文标题: | |
| 文章作者: | LepeCoder |
| 发布时间: | |
| 原始链接: |


