图神经网络知识点梳理（一）

这一系列是对刘知远老师《Introduction to Graph Neural Networks》的阅读笔记，并参考各路神仙大佬的论文和博客，对GNN脉络进行了一次梳理，受益匪浅。作为系列第一篇，本文主要介绍谱域图卷积。

数学基础

Vanilla Graph Neural Networks

简介

如下图所示，Vanilla GNN用于处理无向同质图（Undirected Homogeneous Graph），结点和边都包含特征。

图中的一个结点v由它的自身特征及其邻结点共同定义。Vanilla GNN的目的是为每一个结点学习一个Embedding：{\rm{h}}_{v}，称之为隐状态，其中编码了其自身特征和邻结点的信息。
{\rm{h}}_{v}进一步用来计算结点标签分布的{\rm{o}}_{v}，比如分类器的输出。

模型
Vanilla GNN分别用co[v]和ne[v]表示结点v的边集合和邻结点集合。方法定义了两个带参函数local transition function f和local output function g，分别用来求{\rm{h}}_{v}和{\rm{o}}_{v}：
\mathbf{h}_{v}=f\left(\mathbf{x}_{v}, \mathbf{x}_{c o[v]}, \mathbf{h}_{n e[v]}, \mathbf{x}_{n e[v]}\right) \quad (1.1) \\ \mathbf{o}_{v}=g\left(\mathbf{h}_{v}, \mathbf{x}_{v}\right) \quad (1.2) \\ 其中f接受的四个参数分别是：

1. 结点v的特征{\rm{x}}_v；
2. co[v]的特征{\rm{x}}_{co[v]}；
3. 邻结点的隐状态{\rm h}_{ne[v]}；
4. 邻结点的特征{\rm x}_{ne[v]}。

上述的两个local函数是针对每个结点而言，对所有结点我们可以用\rm{H}，\rm{O}，\rm{X}和{\rm{X}}_N分别表示。四者分别表示所有隐状态、所有输出、所有特征和所有结点特征的堆叠。那么式(1.1)和(1.2)可以进一步表示为：
\mathbf{H}=F(\mathbf{H}, \mathbf{X}) \quad (1.3) \\ \mathbf{O}=G\left(\mathbf{H}, \mathbf{X}_{N}\right) \quad (1.4) \\ F和G分别称为global transition function和global output function，同样，它们也分别是f和g的堆叠版本。
Vanilla GNN迭代更新结点的隐状态：
\mathbf{H}^{t+1}=F\left(\mathbf{H}^{t}, \mathbf{X}\right) \quad (1.5) \\ t表示当前迭代轮数。
不动点理论（此处的不动点理论专指巴拿赫不动点定理Banach's Fixed Point Theorem）保证了Vanilla GNN解的存在和唯一性。
不动点理论是说，对于任意初始隐状态{\rm H}^0，只要F是压缩映射（Contraction Map），{\rm H}^0一定能在若干轮次后收敛到某个固定的点，即不动点。对于压缩映射，这里引用[1]的图例：

https://www.cnblogs.com/SivilTaram/p/graph_neural_network_1.html
上图是说，对于x和y两个点，经过F后转换为F(x)和F(y)。压缩是指经F变换后的新空间一定要比原空间小，可通过如下方式度量：
d(F(x),F(y)) \le cd(x,y),0 \le c \le 1 \quad (1.6) \\ d(\cdot, \cdot)为距离度量函数。如果对迭代过程的每一轮都做如上要求，那么最后的压缩空间会把所有点映射到一个不动点上。

如果我们用范数（norm）做距离度量，式（1.6）可以做如下变换：
||F(x)-F(y)|| \le c||x-y|| \quad (1.7) \\ \frac{{ ||F(x)-F(y)||}}{{||x-y||}} \le c \quad (1.8) \\ 令y=x-\Delta x：
\frac{{ ||F(x)-F(x-\Delta x)||}}{{||\Delta x||}} \le c \quad (1.9) \\ ||F'(x)||=||\frac{{\partial F(x)}}{\partial x}|| \le c ,(0 \le c \le 1)\quad (1.10) \\ 由此可以看到，F的压缩映射等价于令F的梯度/导数小于1。
于是，我们可以用前馈神经网络并对雅可比矩阵施加惩罚项来使F近似压缩映射。
回到Vanilla GNN，它的损失函数为：
\text { loss }=\sum_{i=1}^{p}\left(\mathbf{t}_{i}-\mathbf{o}_{i}\right) \quad (1.11) \\ 其中\rm t为p个有监督结点的标签。再加上需要对雅可比矩阵施加的惩罚项，可以得到目标函数：
J={\rm loss}+\lambda * {\rm max}(||\frac{\partial F}{\partial {\rm h}}|| - c, 0), (0 \le c \le 1) \quad (1.12) \\ 引用原论文[2]的网络架构，可以清晰的回顾上述过程。从下图可以观察到（a）特征只在连通结点之间传播；（b）F和G的参数对所有结点共享且每一轮迭代都是同一组参数。

局限性

1. 效率问题：和RNN等方法不同的是，vanilla GNN需要迭代至收敛，所以迭代次数可能会很大。
2. 参数：vanilla GNN每轮参数一样，表达能力欠缺，
3. 过平滑（over smooth）：如果迭代轮数过大且我们的是关注结点特征的话，过大的轮数会导致过平滑问题，导致所有结点特征都差不多，如Wikipedia上的一张经典的图[3]。

https://www.wikiwand.com/en/Laplacian_matrix
如果我们把上图中每个像素点视为图中的结点，可以看到在迭代开始时有很多不同颜色的结点（颜色差异越大表示特征差异越大），但随着迭代的深入，所有结点的颜色趋于一致。

Graph Convolutional Networks

本部分框架参考张寓弛前辈的博客[7]并做了简化以便于理解，更深刻的解读强烈推荐读一下前辈的博客。笔者为了直观的描述动机，下文暂且放弃了一些严谨性（能省略的都省略了）。

笔者为了直观的描述动机，下文暂且放弃了一些严谨性（能省略的都省略了）。

要想理解GCN以及其后面一系列工作的实质，最重要的是理解其中的精髓Laplacian矩阵在干什么。知道了Laplacian矩阵在干什么后，剩下的只是解法的不同——所谓的Fourier变换只是将问题从空域变换到频域去解，所以也有直接在空域解的（例如GraphSage）。——[7]

拉普拉斯算子是干什么的？

我们从热量\phi(x,t)（也可以理解为能力、状态、信息、特征）传播的角度入手。

如下图，假设我们有四个时刻的热量（将时间离散化了），每一刻的能量受其相邻时刻的能量的影响。

t1时刻的能量可以描述为：
\frac{\partial \phi_{1}}{\partial t}=(\phi_{t2}-\phi_{t1})-(\phi_{t1}-\phi_{t0}) \quad (2.1) \\ 观察右边两项，是两个差分的差分。在离散空间，相邻位置的差分推广到一维连续空间就是导数，那么两个差分的差分推广到一维连续空间就是二阶导。

\phi是关于某个x的函数，所以式（2.1）在一维连续空间中可以改写为：
\frac{\partial \phi}{\partial t}=\frac{\partial^{2} \phi}{\partial x^{2}}\quad (2.2) \\ 进一步推广至高维连续欧氏空间中，可得：
\frac{\partial \phi}{\partial t}=\Delta \phi \quad (2.3) \\ \Delta就是拉普拉斯算子（或者写成\nabla\cdot\nabla,\nabla^{2}）！它代表各个坐标二阶导数的加和。
二维空间：\Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}
三维空间：\Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}}
综上，我们可以看到某个时刻的温度变化可以用拉普拉斯算子衡量，拉普拉斯算子是二阶导对高维空间的推广。

拉普拉斯矩阵是干什么的？

如果我们把上面的一维热量传播路径改成图：

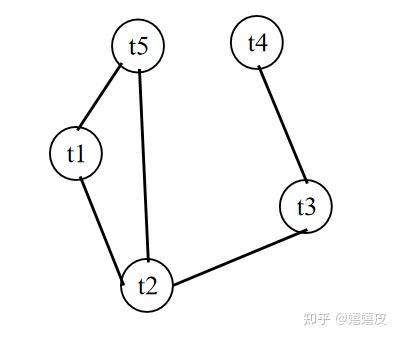
会发现其实是一个道理，不同的是每个时间结点连接的边不止一条。我们可以借助邻接矩阵A来刻画式（2.1）在图中的情景：
\frac{\partial \phi_{i}}{\partial t}=\sum_{j}A_{ij}(\phi_{i}-\phi_{j}) \quad (2.4) \\ 展开：
\frac{\partial \phi_{i}}{\partial t}=\phi_{i}\sum_{j}A_{ij}-\sum_{j}A_{ij}\phi_{j} \\ =deg(i)\phi_{i}-\sum_{j}A_{ij}\phi_{j} \quad (2.5) \\ 再进一步扩展到所有结点上：
\frac{\partial \phi}{\partial t}=D \phi - A \phi = (D-A) \phi = L \phi \quad (2.6) \\ 这个L就是拉普拉斯矩阵！

通过对比式（2.6）和 （2.3）,可以认为：拉普拉斯矩阵等价于离散的拉普拉斯算子。拉普拉斯矩阵描述了物理量的流入/流出；以及二维空间中的温度/特征/信息的传播规律。

对式（2.6）的进一步分析

如果我们进一步把式（2.6）左边一项的时间离散化，可得到：\phi_{t} = \phi_{t-1} + L \phi_{t-1}

这不就是 新自身状态 = 自身状态+聚合的邻结点状态 嘛 ！

那么，在GCN中每个节点状态的变化正比于图拓扑空间中拉普拉斯算子作用在当前的状态。

知道了正比关系这个题，后文就是关于解题方法的内容。

GCN章节的余下内容为：

Spectral Network[6]

（无向图前提下）

图卷积就是把卷积应用到图数据中，而我们也清楚常规的卷积核无法直接应用到图结构中。因为图这种非欧几里得结构的数据无法保持平移不变性。即每个结点的邻结点数目可能不同，无法用同一个尺寸的卷积核进行卷积运算[5]。

一种解法是曲线救国：在谱域（Spectral Domain）进行：

1. 对图和卷积核做傅里叶变换（Fourier Transform）；
2. 然后在傅里叶域中对二者进行哈达玛乘积（Hadamard product）；
3. 最后再将乘积结果做**傅里叶逆变换（Inverse Fourier Transform）**换回去。

上图过程如下图所示：

http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html[4]

上述过程可以描述为函数卷积的傅里叶变换是函数傅里叶变换的乘积。
(f*g)(t)=F^{-1}[F[f(t)] \odot F[g(t)]] \quad (2.7) \\ 其中F表示傅里叶变换，\odot表示哈达玛乘积。f(t)和g(t)时两个时域信号，对应卷积，二者分别表示结点特征和卷积核。

傅里叶变换长啥样[9]？
F(\omega)=\mathcal{F}[f(t)]=\int f(t) e^{-i \omega t} d t \quad (2.8) \\ 其中，f(t)表示信号，e^{-i\omega t}为基函数。该式其实就是拉普拉斯算子的广义特征函数，因为e^{-i\omega t}其实是拉普拉斯算子的特征向量：
\Delta e^{-i \omega t}=\frac{\partial^{2}}{\partial t^{2}} e^{-i \omega t}=-\omega^{2} e^{-i \omega t} \quad (2.9) \\ 所以傅里叶变换相当于换了坐标系（以\{e^{-i\omega t}\}为基向量），是对同一个数学对象在不同坐标系下的不同表达方式，某些情况下，傅里叶变换可以带来计算上的便利。

回到和上文同样的思路，我们将傅里叶变换迁移到Graph中。

拉普拉斯矩阵的优良性质[8]：

1. 半正定，实对称； 2.（实对称矩阵）有n个线性无关的特征向量；
2. （半正定矩阵）特征值非负；
3. （实对称矩阵的）特征向量可以化为两两正交的正交矩阵

拉普拉斯矩阵L可做如下分解：
L=U \Lambda U^{T} \quad (2.10) \\ \Lambda=\left[\begin{array}{ccc} \lambda_{1} & \ldots & 0 \\ \ldots & \ldots & \ldots \\ 0 & \ldots & \lambda_{n} \end{array}\right] \quad (2.11)\\ U=\left(u_{1}, u_{2}, \cdots, u_{n}\right) \quad (2.12) \\对应傅里叶变换(公式(2.8))，我们在图中的离散空间做如下类比：
\hat{f}(t)=\sum_{n=1}^{N} f(n) u_{t}(n) \quad (2.12) \\写作矩阵形式（整个图的N个结点）：
\hat{f}=\left[\begin{array}{c}\hat{f}(1) \\\ldots \\\hat{f}(N)\end{array}\right]=U^{T} f \quad (2.13) \\ 所以，对式（2.7）可以描述为：
\left(f * g\right)=U\left(U^{T} g \odot U^{T} f\right) \quad (2.14) \\我们把U^{T}g记为可学习的图卷积核g_\theta (\Lambda)， \Lambda是特征值构成的对角矩阵。那么最后得到的图卷积就是：
(f*g)=Ug_{\theta} (\Lambda)U^{T}f \quad (2.15) \\ 好了！这就是频域卷积的原始形式了！

The spectral construction, draws on the properties of convolutions in the Fourier domain. In {\mathbb R}^{d}, convolutions are linear operators diagonalised by the Fourier basis {\rm exp}(i \omega \cdot t), \omega,t \in {\mathbb R}^d. One may then extend convolutions to general graphs by finding the corresponding “Fourier” basis. This equivalence is given through the graph Laplacian, an opera-tor which provides an harmonic analysis on the graphs

一些直观的理解
如果把矩阵看作是运动，特征值就是运动的速度，特征向量就是运动的方向。那么式(2.15)就是在学习图中的信息在特征向量规定的方向上以什么速度传播消息最高效。

Spectral Network中将g_{\theta}设定为可学习的对角矩阵(式(2.16))，实际上就是在学习如何最优化图中的消息传播。
g_{\theta} = \left[\begin{array}{lll}\theta_{1} & & \\& \ddots & \\& & \theta_{n}\end{array}\right] \quad (2.16) \\ ☝️局限：

1. 不具备局部特性，卷积运算矩阵Ug_{\theta}U^{T}的结果在所有位置非零。这说明它是一个全局卷积核（CNN中是局部卷积核），无法关注局部信号；
2. 每次前向传播都需要显式计算特征分解Ug_{\theta}U^{T}，计算复杂度为{\mathcal O (n^{2})}。

信号的合成与分析

信号可以看作N维空间中的向量，而向量是由一组基经过线性组合合成的。所以我们也可以把信号看作一组基的合成：
\overrightarrow A = \sum\limits_{k = 1}^N {{a_k} {{{\hat v}_k}}} \quad (2.17) \\ 其中{{\hat v}_k} 为基，{a_k} 为每个basis的系数。我们假设这组基为标准正交基。

当我们想知道每个基的系数大小时，就要用到分析：
a_{j}=\vec{A} \cdot \widehat{v}_{j} \quad (2.18) \\ 实现方式是将信号与对应的基做内积。

举个例子，C(1,0)和B(0,1)是一组标准正交基，向量D(4,2)为这组基的线性组合。D=4C+2B。当我们想知道C的系数时，可以对D和C做内积：(4,2) \cdot (1,0)=4。

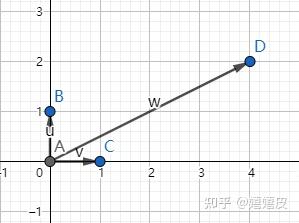
CHEBNET[10]

Spectral Network的卷积核是全局核，随之而来的弊端是较大的计算量。ChebNet通过

Chebyshev多项式对卷积核g_{\theta}进行了近似，增加了卷积的局部特性的同时降低了计算量。

Chebyshev多项式的讲解可以参考[11]。

ChebNet提出，式(2.15)中的卷积核可以用切比雪夫不等式的截断展开式的K阶\mathrm{T}_{k}(x)来近似：
g_{\theta}(\Lambda)=\sum_{k=0}^{K-1} \theta_{k} T_{k}(\tilde{\Lambda}) \quad (2.19) \\ 此时，卷积定义为(Chebyshev多项式只作用在对角矩阵上)：
U\sum\limits_{k = 0}^{K - 1} {{\theta _k}} {\mathrm{~T}_k}(\tilde \Lambda ){U^T} = \sum\limits_{k = 0}^{K - 1} {{\theta _k}} {\mathrm{~T}_k}(U\tilde \Lambda {U^T}) = \sum\limits_{k = 0}^{K - 1} {{\theta _k}} {\mathrm{~T}_k}(\tilde L) \quad (2.20) \\ (f*g) \approx \sum_{k=0}^{K} \theta_{k} \mathrm{~T}_{k}(\tilde{\mathrm{L}}) \mathrm{x} \quad (2.21) \\
其中\tilde{\rm{L}}=\frac{2}{\lambda_{\max }} {\rm L}-{I}_{N}，\lambda_{max}为\rm L的最大特征值。\theta \in {\mathbb R}^{\boldsymbol K}为切比雪夫系数向量。此处限制\rm{L}的范围至[-1,1]是因为第一类Chebyshev形式为：
{\rm T}_k({x})=cos(k \cdot arccos(x)) \quad (2.22) \\ 其输入要求了区间限制。

另外可以看到（2.17）展现了ChebNet不再需要做特征分解的优势。

切比雪夫递推多项式定义为：
\mathrm{T}_{k}(\mathrm{x})=2 \mathrm{x} \mathrm{T}_{k-1}(\mathrm{x})-\mathrm{T}_{k-2}(\mathrm{x}) \quad (2.23) \\ {\rm T}_0({\rm x})=I \quad (2.24) \\ {\rm T}_1(\rm x)=\rm x \quad (2.25) \\ 由上式得到的ChebNet卷积核的localize特性，可以参考[13]。

GCN[12]

GCN对ChebNet做了几步变换。

第一，令K=1，减轻对邻结点的过拟合现象（相比ChebNet，GCN只考虑了一阶邻结点）。

第二，令\lambda_{max} \approx 2，简化计算；

此时式(2.21)可转化为：
(g*x) \approx \theta_{0}x+\theta_{1}({\rm L}-{I}_N)x= \theta_{0}x -\theta_{1}x + \theta_{1}{\rm L}x \quad (2.19) \\ 第三，令\theta=\theta_0=-\theta_1，简化计算；

进一步简化：
(g*x) \approx \theta x + \theta{\rm L}x =\theta(I_N+{\rm L})x = \theta(I_N+D^{-1/2}AD^{-1/2})x \quad (2.20) \\ 第四，renormalization trick：
{\rm Z} \approx {\tilde D}^{-1/2}{\tilde A}{\tilde D}^{-1/2}{\rm X}\Theta \quad (2.21) \\ 其中，{\tilde A}=A+I_{N}，{\tilde D}_{ii}=\sum_{j}{\tilde A}_{ij}。

AGCN[14]

Spectral Network，ChebNet，GCN三者对原始图结构建模，AGCN认为图结构中存在额外的潜在关系值得探究，所以除了原始的拉普拉斯矩阵，AGCN加入了“残差”拉普拉斯{\rm L}_{res}：
\widehat{\mathrm{L}}=\mathrm{L}+\alpha \mathrm{L}_{r e s} \quad (2.22) \\ {\rm L}_{res}形式与{\rm L}一致：
\begin{aligned}\mathrm{L}_{r e s} &=\mathrm{I}-\widehat{\mathrm{D}}^{-\frac{1}{2}} \widehat{\mathrm{A}} \widehat{\mathrm{D}}^{-\frac{1}{2}} \\\widehat{\mathrm{D}} &=\operatorname{degree}(\widehat{\mathrm{A}})\end{aligned} \quad (2.23) \\ 其中\widehat{\mathrm{A}} 是通过可学习的度量函数来计算的。AGCN认为对不同的图拓扑结构应当设计不同的度量函数，借助于Mahalanobis距离：
D\left(\mathrm{x}_{i}, \mathrm{x}_{j}\right)=\sqrt{\left(\mathrm{x}_{i}-\mathrm{x}_{j}\right)^{T} \mathrm{M}\left(\mathrm{x}_{i}-\mathrm{x}_{j}\right)} \quad (2.24) \\ 令{\rm M}={\rm W}_{d}{\rm W}_{d}^{T}使其转化为可学习的度量函数。最后通过高斯核函数和归一化来计算\widehat{\mathrm{A}} 。

参考

1. 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (一)
2. Scarselli, Franco, et al. "The graph neural network model." IEEE transactions on neural networks 20.1 (2008): 61-80.
3. https://www.wikiwand.com/en/Laplacian_matrix
4. http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html
5. 从传统傅里叶变换到图卷积
6. Bruna, Joan, et al. "Spectral networks and locally connected networks on graphs." arXiv preprint arXiv:1312.6203 (2013).
7. https://mp.weixin.qq.com/s/DnRSYtM8aBLL3cBXYT5KBQ
8. 如何理解GCN？
9. 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (二)
10. Defferrard, Michaël, Xavier Bresson, and Pierre Vandergheynst. "Convolutional neural networks on graphs with fast localized spectral filtering." arXiv preprint arXiv:1606.09375 (2016).
11. 最美数学系列-什么是切比雪夫多项式？
12. Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
13. Chebyshev多项式作为GCN卷积核
14. Li R, Wang S, Zhu F, et al. Adaptive graph convolutional neural networks[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2018, 32(1).