卡尔曼滤波算法学习记录

关键节点：

协方差矩阵\(P_{k}\)：因为我们要利用速度与位置的某种关系来预测下一步位置，所以这个协方差矩阵表示的就是二者之间的相关性。简单来说，矩阵中的每个元素\(\sum\nolimits_{ij}\)表示第 i 个和第 j 个状态变量之间的相关度,协方差矩阵通常用\(\sum\nolimits_{}\) 来表示，其中的元素则表示为\(\sum\nolimits_{ij}\)。
最佳估计\(\hat{x}\):即均值，其它地方常用 μ 表示
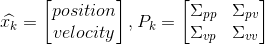
当前状态：k-1时刻
下一状态：k时刻
运动学公式：由运动学公式所列出来的式子可以看做状态转移矩阵
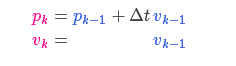
更新协方差矩阵：将分布中的每个点都乘以矩阵 A（用来更新协方差矩阵），下图是协方差矩阵的一个运算性质
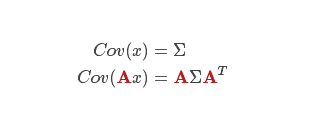
预测过程：状态转移矩阵\(F_{k}\)
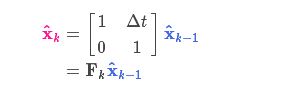
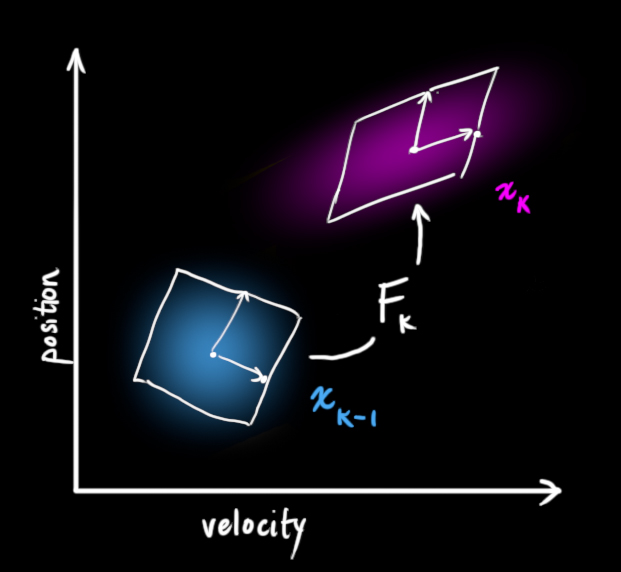
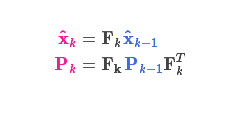
外部控制量：可能存在外部因素会对系统进行控制，带来一些与系统自身状态没有相关性的改变，（以火车的运动状态模型为例，火车司机可能会操纵油门，让火车加速），我们可以用一个向量\(\vec{x_k}\)来表示，将它加到我们的预测方程中做修正。我们知道了期望的加速度α，根据基本的运动学方程可以得到：

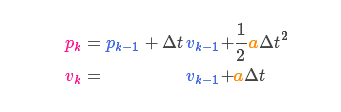
　　以矩阵的形式表示就是：

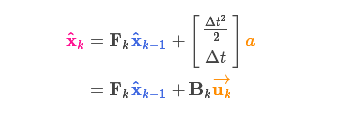
其中：\({B_k}\)称为状态控制矩阵（比如：加速减速如何改变物体的状态），\(\vec{u_k}\)称为控制向量（比如：表明控制的力度大小和方向，对于没有外部控制的简单系统来说，这部分可以忽略）
外部干扰：一些系统之外的干扰，例如飞行器收到风力的干扰，机器人受到坡度的影响在每次预测之后，我们可以添加一些新的不确定性来建立这种与“外界”（即我们没有跟踪的干扰）之间的不确定性模型：

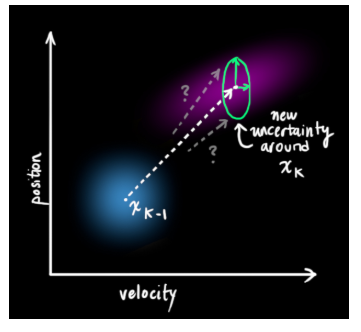
同时，原始估计中的每个状态变量更新到新的状态后，仍然服从高斯分布（包括我们之前没有特别去考虑的外部干扰）。我们可以说\({\hat{x}_{k-1}}\)的每个状态变量移动到了一个新的服从高斯分布的区域，协方差为\({Q_k}\)。换句话说就是，我们将这些没有被跟踪的干扰当作协方差为\({Q_k}\)的\(\color{red}{噪声}\)来处理。

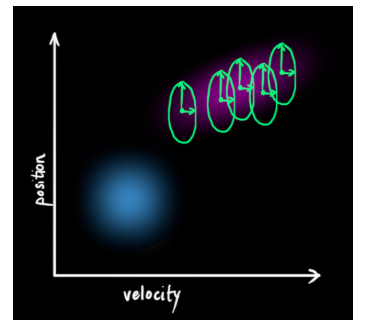
这产生了具有不同协方差（但是具有相同的均值）的新的高斯分布。

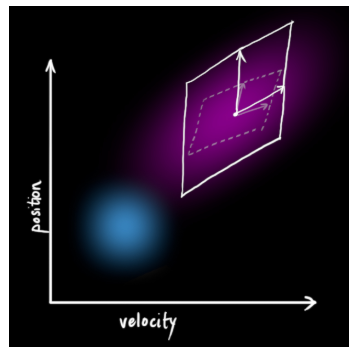
我们通过简单地添加\({Q_k}\)得到扩展的协方差，下面给出预测步骤的完整表达式：

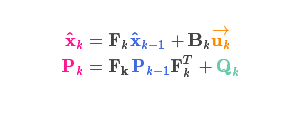
由上式可知，\(\color{#006600}{新的最优估计}\)是根据\(\color{#dd00dd}{上一最优估计}\)预测得到的，并加上\(\color{#660066}{已知外部控制量}\)的修正。
而\(\color{#006600}{新的不确定性}\)由\(\color{#dd00dd}{上一不确定性}\)预测得到，并加上\(\color{#DAA585}{外部环境的干扰}\)。
至此，我们对系统可能的动向有了一个模糊的估计，用这里\(\hat{X_k}\)和\({P_k}\)来表示,此时我们还没有考虑传感器所测量的数据。

用测量值来修正估计值
我们可能会有多个传感器来测量系统当前的状态，哪个传感器具体测量的是哪个状态变量并不重要，也许一个是测量位置，一个是测量速度，每个传感器间接地告诉了我们一些状态信息。同时，传感器读取的数据的单位和尺度有可能与我们要跟踪的状态的单位和尺度不一样，我们用矩阵 \(H_k\) 来表示传感器对原状态所施加的影响。（一般这个 \(H_k\) 取1）

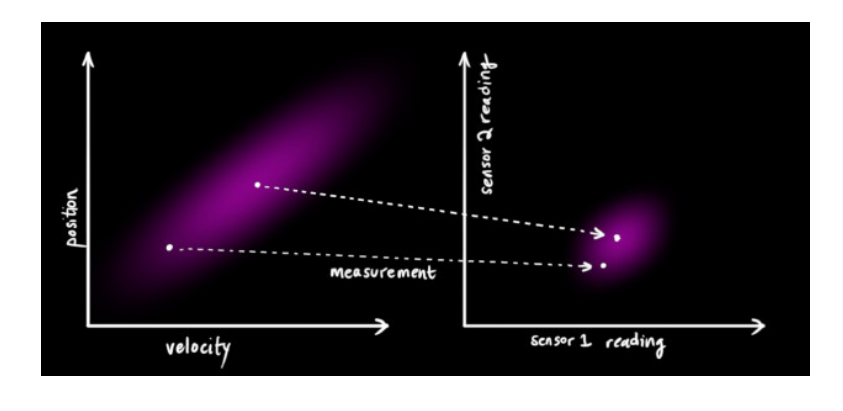
我们可以计算出传感器读数的分布，用之前的表示方法如下式所示：

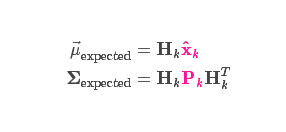
从测量到的传感器数据中，我们大致能猜到系统当前处于什么状态。但是由于存在不确定性，某些状态可能比我们得到的读数更接近真实状态。

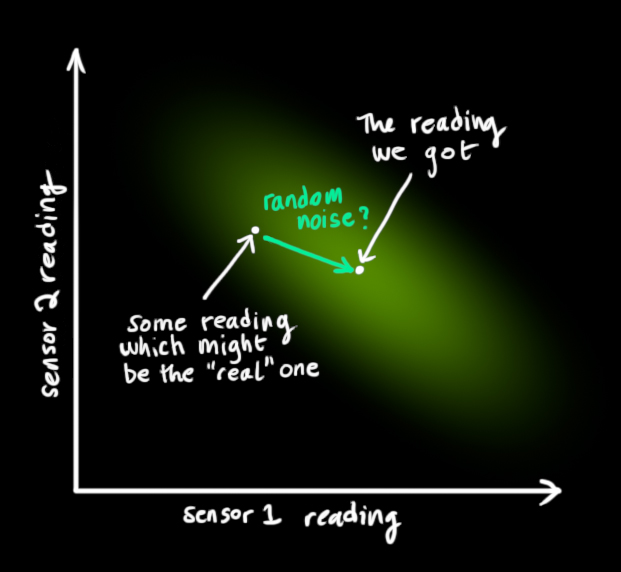
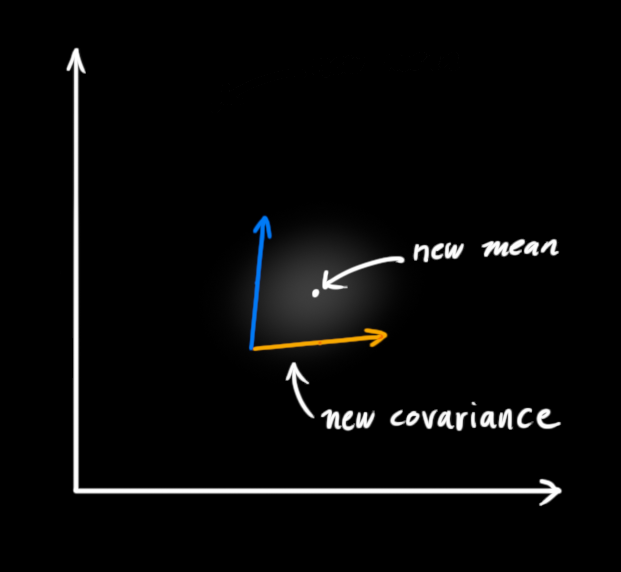
我们将这种不确定性（例如：传感器噪声）用协方差 \(R_k\) 表示，该分布的均值就是我们读取到的传感器数据，称之为 \(z_k\) 。现在我们有了两个高斯分布，一个是在预测值附近，一个是在传感器读数附近。

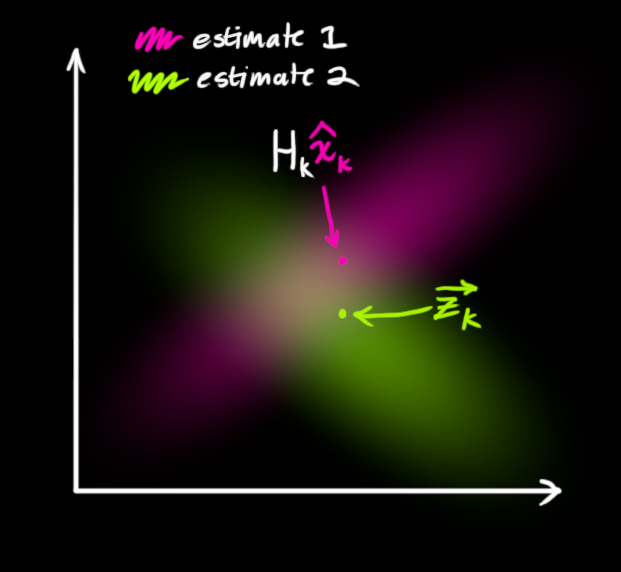
我们必须在预测值(\(\color{#F500B3}{粉红色}\)）和传感器测量值（\(\color{#A8F101}{绿色}\)）之间找到最优解。
那么，我们最有可能的状态是什么呢？对于任何可能的读数 (\(z_1\),\(z_2\))，有两种情况：（1）传感器的测量值；（2）由前一状态得到的预测值。
如果我们想知道这两种情况都可能发生的概率，将这两个高斯分布相乘就可以了。

剩下的就是重叠部分了，这个重叠部分的均值就是两个估计最可能的值，也就是给定的所有信息中的最优估计。
其实，这个重叠的区域就是另一个高斯分布（这里需要用到概率论的部分知识）。

直接给出新的高斯分布的数据：

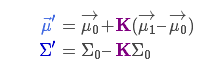
其中： Σ 表示高斯分布的协方差， \(\hat{μ}\) 表示每个维度的均值

且矩阵 \(K\) 称为卡尔曼增益
将上述两个结果进行整合
我们手头现在有两个高斯分布
预测部分：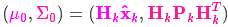
测量部分：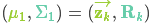
将这两个部分的数据带入新的合成高斯分布：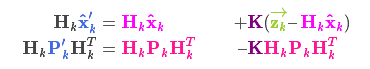
可以求得卡尔曼增益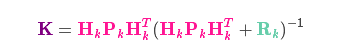
又经过一波化简后我们用这两部分表示出新的合成高斯分布的均值和协方差

其中：
卡尔曼滤波包括两个部分：时间更新与测量更新，且是一个自回归过程
- 时间更新：滤波器使用上一状态的估计，作出对当前状态的估计
为什么要把当前的最优估计看做成一个高斯分布
　答：虽然我们可以根据物体上的设备获得物体的速度，GPS数据，但是系统总是会存在误差，无论是我们的计算还是系统测量上，所以我们只能认为当前状态是当前真实状态的一个最优估计，且符合高斯分布。
协方差矩阵是干啥的？
　答：协方差矩阵用来描述两个随机变量的相似程度
补充理解
　　卡尔曼滤波器允许我们结合当前状态的不确定和它的传感器测量的不确定来理想地降低机器人的总体不确定程度。这两类不确定通常用高斯概率分布或正态分布来描述。高斯分布有2个参数：均值和方差。均值表示最高概率的值，方差表示我们认为这个均值有多大的不确定性。