Causality 基础概念汇总

1. 三层因果关系之梯的公式化描述
2. 因果效应与可识别性（Causal Effects and Identification）
3. 后门准则（Back-door criterion）
4. 前门准则（front-door criterion）
5. 反事实推理 （Counterfactual Infernece）
6. Markov property，Faithfulness与等价类详解
7. 因果发现的相关方法（Causal Discovery CD）
8. CD续：函数化因果模型FCM（Functional Causal Model）
9. DAG,PAG,MAG三种因果图的区别与作用

1：三层因果关系之梯的公式化描述^[1]

给定下面的结构化因果模型

• Prediction（如果他用药了能恢复的概率）: P(R|T)=\sum_S P(R|T,S)P(S|T)
• Intervention（如果我们强制他用药，他能恢复的概率）： P(R|do(T))=\sum_SP(R|T,S)P(S) ，相比较预测而言，这里因为切断了 S,T 之间的联系，使得二者相互独立，因此才将 P(S|T) 换为 P(S) 。
• Counterfactual（给定people用药了病也好了，那么如果它没用药会恢复吗？）

可以看到prediction会受到可能会受到采样的特殊分布的影响从而产生辛普森悖论等相关现象，比如下图中在small，large stone中接受治疗都会带来正面的影响，但是将样本混合起来反而会看到负面的影响（small stone的Treatment B样本实在太多了，而prediction本质又是计算平均）。而intervention就不会产生类似的现象

2：Causal Effects and Identification

所谓的Causal Effects可以简单的理解为我们的intervention，即 X 对 Y 的因果效应表示为 P(Y|do(X)) ,具体一点可以写为如下形式

P(Y=y|do(X=x))=\sum_zP(Y=y|X=x,PA(X)=z)P(PA(X)=z)

其中 PA(X) 表示 X 的父节点， z 遍历这些父节点可能取值的所有组合。而因果效应的可识别性，简单来说就是判断model的解是否唯一。

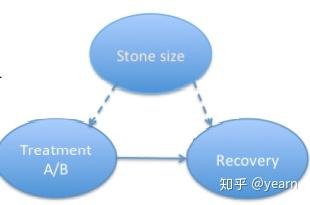
我们给定因果图和可观测变量分布（假设Stone Size的分布不可知，我们只有 T,R 的分布），那么问题就是：我们是否可以恢复出 T\rightarrow R 的因果效应。也就是说，当前面两个条件给定时，如果所有model计算出的 P(Y|do(X)) 都是一致的，也就是我们能得到一个unique的解。

3：后门准则^[2]

如果整个 DAG 的结构已知且所有的变量都可观测，那么我们可以根据上面 do 算子的公式算出任意变量之间的因果作用。但是，在绝大多数的实际问题中，我们既不知道整个 DAG 的结构，也不能将所有的变量观测到。因此，仅仅有上面的公式是不够的。

下面，我将介绍 Judea Pearl 提出的 “后门准则”（backdoor criterion）和“前门准则”（frontdoor criterion）。这两个准则的意义在于：（1）某些研究中，即使 DAG 中的某些变量不可观测，我们依然可以从观测数据中估计出某些因果作用；（2）这两个准则有助于我们鉴别“混杂变量” 和设计观察性研究。

前门准则和后门准则，都涉及了 d 分离（d-seperation）的概念。

定义（ d 分离）: 设 X，Y，Z 是 DAG 中不相交的节点集合， \pi 为一条连接 X 中某节点到 Y 中某节点的路径 （不管方向）。如果路径 \pi 上某节点满足如下的条件：

1. 在路径 \pi 上，w 点处为 V 结构 （或称冲撞点 X\rightarrow w\leftarrow Y ，collider），且 w 及其后代不在 Z 中；(因为对collider关系， w 不可观测时 X,Y 相互独立)
2. 在路径 \pi 上， w 点处不是 V 结构，且 w 在 Z 中,

那么称 Z 阻断 (block) 了路径 \pi 。进一步，如果 Z 阻断了 X 到 Y 的所有路径，那么称 Z d 分离 X 和 Y ，记为 (X⊥Y|Z)_G 。

下面介绍 Pearl (1995) 的主要工作：后门准则和前门准则。

后门准则（）：在 DAG 中，如果如下条件满足：

1. Z 中节点不能是 X_i 的后代；
2. Z 阻断了 (X_i,Y_j) 之间所有指向 X_i 的路径（这样的路径可以称为后门路径）；

则称变量的集合 Z 相对于变量的有序对 (X_i,Y_j) 满足后门准则。进一步，若 Z 相对于变量的有序对 (X_i,Y_j) 满足后门准则，其中 X_i 和 Y_j 是 X 和 Y 中的任意节点；那么称变量的集合 Z 相对于节点集合的有序对 (X,Y) 满足后门准则。

Pearl (1995) 证明，若存在一个变量集合 Z 相对于 (X,Y) 满足后门准则，那么 X 到 Y 的因果作用是可以识别的，且

P(y|do(X)=x)=\sum_zP(y|x,z)P(z)\\

从上面可以看出，上面的后门准则和可忽略性假定下 ACE 的识别公式一样：都是用 Z 做调整 (adjustment)，先分层再加权求和。这条结论在 Rosenbaum and Rubin (1983) 之后提出，且流行病学家也都用这样的调整方法控制混杂因素，因此对很多统计学家和流行病学家来说并不新奇。比较新颖的结论是下面的前门准则。

4：前门准则

前门准则：在 DAG 中，称节点的集合 Z 相对于有序对 (X,Y) 满足前门准则，如果

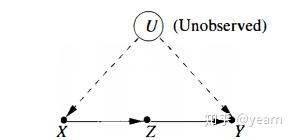
1. Z 切断了所有 X 到 Y 的直接路径；
2. X 到 Z 没有后门路径；
3. 所有 Z 到 Y 的后门路径都被 X 阻断。

此时，如果 P(x,z)>0 ，则 X 到 Y 的因果作用可识别，为

P(y|do(X)=x)=\sum_zP(z|x)\sum_{x'}P(y|x',z)P(x')\\

这个前门路径看似很难理解，证明似乎很不直观，恰似变魔术。但是它其实是很显然的，在前门路径的 DAG 中，我们有：（1） X 对 Z 的因果作用可识别，因为它们之间没有后门路径；（2） Z 对 Y 的因果作用可识别，因为 X 阻断了他们的后门路径；（3） X 对 Y 的作用，仅仅通过 Z 而产生。这三点蕴含着 X 对 Y 的因果作用可识别—这样看来，这个结论就不奇怪了！

Pearl 在书中讲了一个非常有趣的例子，来说明前门准则的用处。

例子：我们关心吸烟 X 和肺癌 Y 之间的因果关系。由于一个潜在的不可观测的基因 U 的存在，吸烟和肺癌之间有一条 “活” 的后门路径，因此不借助其他的条件，我们无法识别吸烟与肺癌的因果关系。如果我们有这样的知识“吸烟 X 仅仅通过肺部烟焦油的含量 Z 来影响肺癌 Y ”，那么吸烟对肺癌的因果作用就可以估计出来了。不过，这里需要两个条件，也就是在证明中使用的两个条件独立性，他们表明：（1）吸烟 X 和肺部烟焦油的含量 Z 之间没有 “活” 的后门路径（或者没有混杂因素）；（2）吸烟 X 对肺癌 Y 的作用仅仅来源于吸烟 X 对肺部烟焦油 Z 的作用，或者说，吸烟 X 对肺癌 Y 没有 “直接作用”。

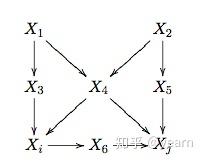
例子：在 上图 的 DAG 中， (Xi,Xj) 之间的后门路径被 \{X3,X4\} 或者 \{X_4,X_5\} 阻断，而前门路径被 X_6 阻断。上面的两个准则表明，要识别从 X_i 到 X_j 的因果作用，我们不需要观测到所有的变量，只需要观测到切断后门路径或者前门路径的变量即可。

5：反事实推理^[3]

Counterfactual 反事实^[4]，对应于极具智慧的人类文明，也是因果之梯的顶峰。counterfactual和干预intervention区分的关键在于“hindsight”(事后来看)，即反事实强调在对结果已知观测的基础上再对反事实的问题进行解答：“假如当时发生的与实际情况不同，结果会怎样？”，这就要求一种对虚构世界的推理能力。另一方面，Intervention关注的更多是群体的总效应或者平均因果效应。而反事实更关注特定事件或个体层面的因果关系。举个栗子，比如Intervention解决的是“吸烟是否导致肺癌”，而counterfactual研究的是“我的外公30年来每天一支烟，假如他不曾吸烟的话，他会活多久”，这两者之间是具有很大差别的。另外可能有小伙伴会问：为什么在因果之梯图中，科学发现是一种反事实呢？其实我们人类不断总结的各种科学定理很多就是反事实的体现，比如当人类发现胡克定律（F=-k·x ）之后，给定弹簧伸长量我们就能相应的推断出力的大小，即使这个伸长量可能并未被实际观察到过。

反事实推理的过程可以分为三个步骤

6:Markov property，Faithfulness与等价类详解^[5]

马尔可夫性（Markov property）是构成图模型基础的一个常用假设。当一个分布关于一个图是“马尔可夫”（Markovian）的，则表明这个图能够建模分布中的某些特定的独立性，那么我们就可以利用这些独立性来进行有效的计算或进行数据存储。有向图和无向图都存在马尔可夫性，但在因果推理中，主要还是研究有向图的马尔可夫性。

【定义】马尔可夫性：给定一个有向无环图 G 以及所有节点的联合概率分布 P ，那么如果 X_i 和 X_j被 S d分离\Rightarrow X_i \perp\!\!\!\!\perp X_j|S ，则称这个分布 P 满足关于G 的全局马尔可夫性。

与之相对偶的性质是忠实性（Faithfulness）。

【定义】忠实性：考虑一个分布 P 和一个有向无环图 G ，那么如果 X_i \perp\!\!\!\!\perp X_j|S\Rightarrow X_i 和 X_j被 S d分离 ，那么 P 关于 G 就是忠实的。

考虑如下的一个例子。假设概率分布 P 对有向无环图 G 是马尔可夫且忠实的，那么根据以下条件确定模型 G 的结构。

1. X \perp\!\!\!\!\perp Z （变量包括 X 、 Y 、 Z ）
2. X \perp\!\!\!\!\perp Y|Z （变量包括 X 、 Y 、 Z ）
3. X \perp\!\!\!\!\perp Y 、 X \perp\!\!\!\!\perp W|Z 、 X \perp\!\!\!\!\perp W|Z, Y 、 Y \perp\!\!\!\!\perp W|Z 、 Y \perp\!\!\!\!\perp W|Z, X （变量包括 W 、X 、 Y 、 Z ）

三种条件下的答案如图1所示。第1个条件的情形是唯一的对撞结合，也就是V结构。根据之前学习的知识，对撞结合让 X 和 Z 独立，当以 Y 为条件时， X 和 Z 变为相关。第2个条件符合的结合不止一种。这三种结构被称为马尔可夫等价类（Markov Equivalence class）。

【定义】马尔可夫等价类：如果有向无环图 G 和 H 具有相同的d分离特性，那么 G 和 H 就是马尔可夫等价的，并且同属于一个马尔可夫等价类。如果 G 和 H 是马尔可夫等价的，那么它们具有相同的骨架（Skeleton）和V结构（也即对撞结构），反之亦然。

骨架的意思可以理解为不考虑箭头方向的连接结构。图1(i)和(ii)的四个图都共有相同的骨架。图1(ii)的三个图不仅具有相同的骨架，还具有相同的V结构（因为它们都没有V结构），所以它们属于同一个马尔可夫等价类，但是它们同图1(i)的图就不是同一个马尔可夫等价类，因为(i)中有一个V结构。

如果分布 P 对于可能的有向无环图 G 是马尔可夫且忠实的，那么图 G 中的d分离语句与分布中相应的条件独立性语句就可以建立一一对应的关系。因此，在图 G 的马尔可夫等价类之外的所有图都可以被排除。但同属于一个马尔可夫等价类的图是无法区分的。

7：Causal Discovery^[6]

1. 何谓因果发现^[7]

众所周知，在统计学中，因果关系意味着相关性，但相关性并不意味着因果关系。也许更准确的说法是，相关性并不直接意味着因果关系----实际上，研究已经表明，在满足各种假设下，至少得到在某种程度上，一组随机变量的潜在因果结构可以从观测数据中发掘出来。自20世纪90年代以来，研究者已利用数据中的条件独立关系来发掘潜在的因果结构。典型的基于（条件独立）约束的算法包括PC和fast causal inference（FCI）。PC假定没有混杂因素（confounder）（两个测量变量未观察到的直接的共同因），且其发掘的因果信息是渐近正确的。即使存在混杂因素，FCI也能给出渐近正确的结果。这种方法应用广泛，因为只要有可靠的条件独立性测试方法，它们可以处理各种类型的数据分布和因果关系。然而，它们不一定能提供完整的因果信息——它们一般输出一组满足相同条件独立性的因果结构，它们都包含在对应的（独立）等价类中 。

PC和FCI算法可以得到这些等价类的图形表示。在没有混杂因素的情况下，基于得分的算法旨在通过优化恰当定义的得分函数(score function)来发掘因果结构。其中，greedy equivalence search（GES）是一个众所周知的两阶段方法，它直接在等价类空间中搜索。其并行化版本（FGES）能够在很高维的数据集中搜索因果关系。 这些算法已经在Tetrad软件包中实现了(htp://http://www.phil.cmu.edu/tetrad/)。

2. 因果发现算法及其假设

下面简要介绍基于条件约束 (constraint-based) 的因果发现算法和基于评分 (Score-based approach) 的因果发现算法。

（1）基于条件约束的因果发现算法

首先需要了解马尔可夫条件和faithfulness假说，该假设可以在因果图结构和统计独立性之间建立一个对应关系。特别是在无环图的情况下，这种映射是一对一的。因此我们可以通过判定观测变量之间的条件独立性来学习因果结构。

马尔可夫条件说的是任何变量，给定其父节点，都和它的非后代 (non-descendants) 统计独立。上图中给定X, Z和Y是统计独立的。马尔科夫条件提供了如下蕴含关系：结构图中表示的独立性->概率独立性， 或者等价地：概率依赖性->结构图中表示的依赖关系。值得一提的是，马尔科夫条件在一般情况下都是满足的，但在量子物理中需要更进一步的研究。

为了在因果图结构和概率独立性之间建立一个对应关系，我们不仅需要马尔科夫条件，还需要faithfulness假说。它说的是：所有观测到的概率条件独立性都包含在马尔科夫条件中。也就是它提供了如下的蕴含关系：概率独立性->结构图中表示的独立性， 或者等价地：结构图中表示的依赖关系->概率依赖性。

这一类算法中比较有代表性的：PC算法^[8]伪代码如下

输入：一个代表图模型节点的随机变量集合V；条件独立性信息；统计检验显著性水平\alpha。
输出：部分的完备有向无环图CPDAG\tilde{G}，分隔变量集合\tilde{S}，以及边的方向。

1. 构造随机变量集合V的完全的联通图（所有节点相连接），利用显著性水平\alpha对相邻的统计变量集合进行条件独立性检验，如果存在条件性独立，就将两个变量之间的边去除掉。
2. 确定V结构（确定方向），树立剩余的边。

1. Step I： X,Y 是邻接的当且仅当它们依赖于剩余变量的每个子集，举个栗子， C\bot D|B 因此C,D之间的边会被去掉。
2. Step II：Orientation propagation：挖掘v结构，具有 Y-X-Z 形式的Markov等价类。

但是有时候，仅仅通过独立性你会得到一些互相冲突的结论，比如下图中如果我们依靠faithful假设，那么 X_1\rightarrow X_2 \leftarrow X_4 应该形成 V 结构才能保证 X_1,X_4 边缘分布独立，但这样又会使得 X_2,X_3 边缘分布不独立，因此这时必然存在confounder。这是PC算法无法处理的

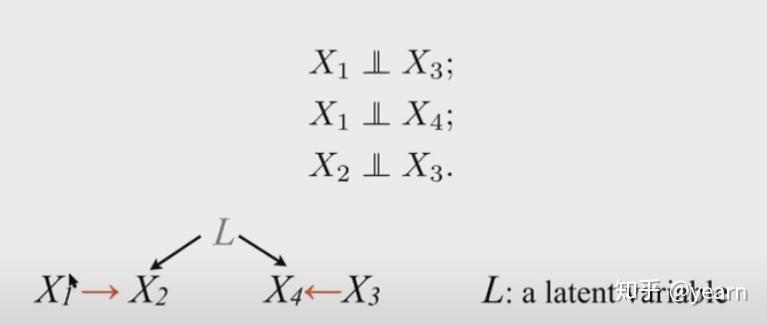
此时FCI（Fast causal inference）算法应运而出，允许得到的因果图不是DAG，而是PAG，使用如下组件定义因果图，允许confounder的存在

(2)基于评分的算法：GES

• 贝叶斯网络结构学习问题看成是优化问题，通过给定结构的评分函数，利用搜索算法，寻找评分最优的网络结构。

确定网络结构，数学模型：

\max f(G,D)\; s.t. G\in\Omega,G|=C\\

• 其中 f 是结构评分函数， \Omega 是结构空间， G|=C 表示G 满足约束条件C。在搜索评分过程中，其约束条件C是要求所搜索到的结构满足结构图中无环。
• 给定训练数据D及一个可能的结构G,如何去计算其评分 f(G, D) 。如果评分函数能够满足一些特性如一 致性，则其评分效果更佳

GES (greedy equivalent search)算法

• 从一个空图出发，采用两个不同的搜索阶段来寻找评分最高的结构。
• 采用贪心前向搜索法( GFS )来不断地在空图中加边，直至评分值无法提高为止;
• 利用贪心反向搜索法( greedy backward search， GBS )在图中不断地删除边，直至评分值不能提高为止。

8：函数化因果模型FCM（Functional Causal Model）^[9]

最近研究显示，基于恰当定义的函数因果模型（functional causal models，FCM）能够在同一个等价类中区分不同的有向无环图（DAG）。这种优势来自除了条件独立关系之外的对数据分布或因果过程的附加假设。FCM将果变量（effect variable） Y 表示为直接原因 X 和一些噪声项 E 的函数，即 Y= f(X，E) ，其中 E 与 X 之间独立。多亏了受限函数类（constrained functional classes），X和Y之间的因果方向变得可以识别——！这是因为在正确的因果方向上噪声和因果之间才满足独立条件，而在错误的因果方向则不满足！。典型的FCM包括

• 线性非高斯无环模型（LiNGAM），其中 Y = aX + E （ a 是线性系数），
• 非线性（PNL）因果模型，其因果过程 Y = f_2(f_1(X)+ E) 中考虑了因的非线性效果以及可能的非线性传感器或测量失真 f_2 ，(最general的模型)
• 非线性加性噪声模型（ANM），其中 Y= f(X)+ E。

因果方向的可识别性是函数因果发掘（functional causal discovery）中的关键问题。基于PNL因果模型的因果方向可识别的条件亦适用于LiNGAM和ANM，因为后面两个是PNL因果模型的特例。假设数据是根据PNL因果模型生成的，而且相关函数是平滑的且X和E密度函数处处为正，那么只在五种特定情况下，其因果方向是不可识别的。相应地，基于FCM从观测数据中估计因果结构的一种方法是先在给定数据上拟合模型，然后测试估计出的噪声项与假设的原因之间的独立性。到目前为止，函数因果发掘主要关注没有混杂因素或反馈的情况，不过也有少数例外。

DAG,PAG,MAG三种因果图的区别与作用^[10]

Directed Acyclic Graph (DAG)

有向无环图对于顶点集合 \mathbf{V} 可以给出两种不同的解释。一方面，这样的图可以用来表示变量之间的因果关系， G 中从A到B的一条边意味着A是B相对于 V 的直接原因。给出这样的解释后，因果图就是一个DAG。

另一方面，一个顶点集合 V 的DAG也可以表示 V 上的一组概率度量，如果这个图满足局部Markov property的话。

DAG存在两个问题

1. 隐变量的存在使得即使因果图完全已知，我们也无法预测干预分布，因为我们只有可观测变量的边缘数据分布，而不是所有因果变量的联合分布。即在一个带有潜在变量的因果DAG下，干预后的概率是不可识别的。
2. 因果结构很少是完全一致的，大多数情况下我们只能依靠观测数据来推测因果结构，而观测数据很少能确定唯一的因果结构。现有的CI方法得到的往往是等价类，而这些等价类在 do 算子d额作用下答案却不一定相同。考虑两个Markov equivalent Graph X\rightarrow Y\rightarrow Z 和to X\leftarrow Y\rightarrow Z 他们表达了一个条件独立关系 X\bot Z|Y ，但是如果我们对graph进行干预会得到不一样的结果。比如对 X 进行干预 do(X=x) ，那么前一个graph得到的 Y 的概率是以 X=x 为条件的概率分布，但是后一个graph得到的 Y 的概率与干预前相同。因此该干预分布并不是可识别的。

Ancestral Graphical Models

祖先图的动机是需要表示可能涉及潜在混杂因素和/或选择偏差的数据生成过程，而不明确地建模未观察变量。

Mixed Ancestral Graphs (MAGs)

一个混合图包含两种边，单向 \rightarrow 或者双向 \leftrightarrow ，两个点之间最多有一条边，边显然有两种端点， -, >。 X\rightarrow Y 称为parent/child关系， X 是parent， X\leftrightarrow Y 称为spouse关系。X 是 Y 的祖先，当且仅当存在一条有向的路径（注意spouse关系可不是有向路径哈）。然后，父亲，孩子，配偶，祖先，子孙关系分别表示如下

\mathbf{Pa_{\mathcal{G}},Ch_{\mathcal{G}},Sp_{\mathcal{G}},An_{\mathcal{G}},De_{\mathcal{G}}}\\

一个direct cycle定义为： Y\rightarrow X\text{ and }X\in \mathbf{An}_\mathcal{G}(Y) 。一个almost directed cycle定义为： Y\leftrightarrow X\text{ and }X\in \mathbf{An}_\mathcal{G}(Y) .

给定一个点集 \mathbf{L} ，和他相关的一条inducing path定义如下：（i）所有不在 \mathbf{L} 中的点（不包括端点）都是路径上的一个冲撞点（ A\rightarrow B\leftarrow C 这里B就是collider）。（ii）每一个collider都是路径端点的祖先（由于对端点没有限制，因此只有两个端点的一条路径是相对于任何集合的inducing path）。在下图(a)中，路径 <C,B,D> 是一个相对于 \{B\} 的inducing path但并不是相对于空集的induce path（因为B并不是一个collider）。 <C,A,B,D> 是相对于空集的inducing path，因为A,B都是路径上的collider，而且A是D的祖先，B是C的祖先。

一个mixed graph被称为是maximal ancestral graph如果：

1. 图不包含任何有向或几乎有向的环（direct/almost direct cycle）
2. 任意两个不相邻的顶点之间不存在inducing path。

第一个条件是DAG的拓展，意味着，箭头，无论是在有向边还是双向边上，都暗示着非祖先地位。第二个条件被称为maximality。上图显然不是一个MAG，因为 C,D 不相邻，但是二者之间有一条inducing path。幸运的是，每一个non-maximal ancestral graph都有一个唯一的超图（supergraph）是MAG。比如上图的超图就是(b)。

在DAG中d-seperation的概念刻画了其中隐含的条件独立性，将其拓展到MAG中就称之为m-seperation

在一个mixed graph中，一条 X,Y 之间的路径p是相对于一组节点 Z 活跃的（m-connecting）如果以下条件满足：
1：p中每一个non-collider都不是 Z 的成员。
2：p中每一个conllider都是 Z 中某成员的祖先。
如果 X,Y 相对于 Z 之间没有活跃路径，则称 X,Y 被 Z m-分离。两个不相交集合 \mathbf{X,Y} 被 \mathbf{Z} m-分离当且仅当 X,Y 之间的每个变量对都被 \mathbf{Z} m-分离。

通过m-分离我们定义了祖先图的马尔可夫性。那么回到最初的起点，我们用祖先图是为了表示涉及的潜在变量，MAG如何完成这个功能呢？给定在变量 \mathbf{V=O\cup L} 的一个DAG \mathcal{G} ,O表示可观测变量，L表示隐变量。我们能找到一个在可观测变量O上的MAG，使得对于任意不相交的 \mathbf{X,Y,Z\subseteq O} ，在 \mathcal{G} 中\mathbf{X,Y} 被 \mathbf{Z} d-分离当且仅当他们在 MAG 中被 \mathbf{Z} m-分离，构造过程如下

\text{Input: a DAG }\mathcal{G}\text{ over }<\mathbf{O,L}>\\ \text{Output: a MAG }\mathcal{M_G}\text{ over }\mathbf{O}\\

1. 对每一对变量 A,B\in\mathbf{O} ,他们在 \mathcal{M_G} 中邻接当且仅当在 \mathcal{G} 中，二者有一条相对于点集 \mathbf{L} 的inducing path。
2. 对每一对邻接变量， A\rightarrow B 表示A是B的祖先， A\leftarrow B 表示B是A的祖先，否则记作 A\leftrightarrow B 。

可以看出， \mathcal{M_G} 确实是一个MAG，而且代表了对O的边缘独立性模型。不同的DAG可能对应相同的MAG，所以本质上，一个MAG代表了一组具有完全相同的d分离结构和可观察变量之间的祖先关系的DAG。因此，因果MAG带有关于真正因果DAG的不确定性，但同时也揭示了基础因果DAG必须满足的特征。所以MAG中的边是什么意思呢？单向边即代表因果关系，双向边代表两个点之间有共同的因，即DAG中有隐变量直接影响两个点。

举个栗子，下图是个DAG，相对应的因果MAG如图(a)所示——在本例中，它恰好是一个DAG。这个MAG也可以代表一些其他的DAGs。例如，PSH和S具有common cause。

Partial Ancestral Graphs (PAGs)

一般来说，MAG仍然不能完全用观测数据进行构造。就像不同的DAGs可以共享完全相同的d分离特征，从而产生完全相同的条件独立约束，不同的MAGs可以产生完全相同的约束条件，因为共享m分离准则。这被称为马尔可夫等价类。就像DAGs的情况一样，所有的马尔可夫等价MAGs都有相同的邻接并且通常也有一些公共的边方向。例如，上图中的两个MAGs是马尔可夫等价的。

PAG用于表示一组等价类的子集，他的端点不像MAG，PAG拥有丰富的端点表示方法（除了下图外，还有一种带下划线的局部限制信息 A*-\underline{*B*}-*C 表示B不是一个collider）。在这里我们定义 X,Y 之间的possibly directed path， <X=V_0,...,V_n=Y> ,对于所有的 0<i\leq n ， V_{i-1},V_{i} 之间的边不是指向 V_{i-1} 的（有向路径的定义为前者一定是指向后者的，这里放宽了约束），此时称X是Y的possible ancestor。

他比较正式的定义如下：

记 [\mathcal{M}] 是一个任意的MAG \mathcal{M} 的一组Markov equivalence class，那么对于这一组等价类的partial ancestral graph \mathcal{P_{[M]}} 是一个满足以下条件的部分混合图：
i. \mathcal{P_{[M]}} 和 [\mathcal{M}] 的任意MAG有相同的邻接关系
ii. 当且仅当 [\mathcal{M}] 中的所有MAGs共享箭头标记 > 时，该箭头才会PAG中出现。
iii. 当且仅当 [\mathcal{M}] 中的所有MAGs共享尾部标记 - 时，该尾部才会PAG中出现。

PAG代表了一个MAG的等价类，显示类中所有成员共享的所有公共边缘标记，并为那些不共享的标记显示圆圈，上图中两个等价的MAG的PAG如下所示

不同的PAG，代表不同的等价类的MAGs，包含了不同的条件独立约束集。因此，PAG原则上是完全可由观察变量之间的条件独立性关系进行测试的。假设Markov condition以及Faithfulness condition成立，现在已经有很多工作能够学到PAG。

在这里路径中的collider的定义为 A*\rightarrow B\leftarrow *C ,再给出两个定义之后会用到

Definite m-connecting path：在PAG中，如果路径p上的每个非端点顶点都是一个明确的非non-collider或者一个collider，那么在两个顶点X和Y之间的路径p相对于一个(可能为空的)顶点集合Z (X,Y \notin Z) 是一个确定的m连接路径，如果以下条件满足
i. 路径上每个non-collider都不是 Z 的成员。
ii. 路径上每个collider都是Z中某些成员的祖先。

不难看出如果PAG中两个点 X,Y 对于 \mathbf{Z} 之间有一条明确的M-连接路径，那么在其表示的所有MAG中这个路径都存在。还有一个推论，如果在MAG中存在给定Z的X和Y之间的m连接路径，那么在PAG中，给定Z的X和Y之间一定存在明确的m连接路径(不一定是相同的路径)。

相对应的，我们将限制条件放宽

Possibly m-connecting path：不约束非端点顶点是collider或者non-collider，第二个约束改成路径上每个collider都是Z中某些成员的possible ancestor。

最后，新开了github整合自己OOD和causality方面的阅读笔记，欢迎关注。

参考

1. ^https://www.youtube.com/watch?v=R4JGk4JyrHw&ab_channel=10-708PGM
2. ^https://cosx.org/2012/10/causality5-causal-diagram/
3. ^https://www.cs.cmu.edu/~epxing/Class/10708-20/lectures/lecture17-Causality1.pdf
4. ^https://zhuanlan.zhihu.com/p/111306353
5. ^https://zhuanlan.zhihu.com/p/127831016
6. ^https://swarma.org/?p=21085
7. ^https://swarma.org/?p=21085
8. ^https://zhuanlan.zhihu.com/p/56210940
9. ^http://www.360doc.com/content/18/0328/19/43535834_741055103.shtml
10. ^Heuristic Greedy Search Algorithms for Latent Variable Models